旧制高等学校について
旧制高等学校は、現在の高等学校とはまったく違うものである。旧制中学を卒業した男子学生が入ることになっている。旧制では、小学が6年、中学が5年だったので、学齢通りに行けば、旧制中学卒業時点では、17歳ということになる。ただ、旧制高等学校は旧制中学4年修了時でも受験することができたので、その場合16歳ということになる。
第一高等学校は、旧制高等学校の中でも最難関校として知られていた。海軍兵学校などと並んで、当時の秀才が集まったとされている。
其一
まずは、1つ目の大問から。2つのあまり関連がない小問から成り立っている。
注意 1. 解答ハ算術、代數、幾何何レノ方法ニヨルモ、又コレ等ヲ混用スルモ可ナリ。
1. 二ツノ直角三角形ABC, ABDガ斜邊ABヲ共有シテ其ノ兩側ニアルトキA, BノCD上ニ於ケル正射影ヲ夫々E, FトスレバCE=DFナルコトヲ證明セヨ
2. 一ツノ四邊形ノ與ヘラレタル頂點ヲ過ル直線ニヨリテ此四邊形ヲ二等分セヨ
問題文が文語体で書かれているために分かりづらいかも知れないが、それほど難しいことを問うているわけではない。小問の1番は、「2つの直角三角形ABC, ABDが斜辺ABを共有し、CとDがABに対して別々の側にあるとき、A, BからCDに垂線を下ろしたときの脚をそれぞれE, Fとする。このとき、CE=DFとなることを証明せよ」ということだ。図にすると、次のようになるだろう。
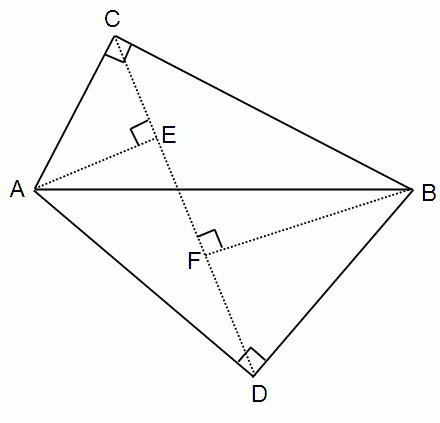
証明を簡単に書いてみると、次の通り。
∠ACB=∠ADB=90° より、四角形ACBDは線分ABを直径とする円に内接する。円周角なので、∠ABD=∠ACD (=∠ACE) となる。また、∠AEC=∠ADB=90° となる。よって、2角が相等しいので、△AEC∽△ADB となる。同様にして、△ABC∽△DBF が導かれる。
△AEC∽△ADB より、AC:CE = AB:BD なので、CE = AC・BD/AB である。また、△ABC∽△DBF より、AB:AC = BD:DF なので、DF = AC・BD/AB であるから、CE=DF となる。
小問の2番は、「四角形に対して、その任意の頂点を通る直線で、この四角形の面積を二等分せよ」ということだ。四角形と等面積の三角形を作図して、その三角形の面積を二等分するだけの簡単な問題だ。
其二
2番目の大問は、代数についての問題。これもそれほど難しくない。
注意 1. 解答ハ算術、代數、幾何何レノ方法ニヨルモ、又コレ等ヲ混用スルモ可ナリ。
3. 方程式 x2+ax+b = 0 ノ二根ニ夫々1ヲ加ヘタルモノガ方程式 x2-a2x+ab = 0ヲ滿足ストイフ。初メノ方程式ノ根ヲ索メヨ。但 a≠1 ナリトス
4. 相異ナル四ツノ正數 a, b, c, d ガ比例スルトキ a ヲ最大トスレバ a+d ハ b+c ヨリ大ナルコトヲ證明セヨ
其三
最後の大問は、文章題である。条件の設定がややこしいが、落ち着いて方程式を立てればなんということもない問題。現代なら、中学校の数学で習う知識で十分対応できる。
注意 1. 解答ハ算術、代數、幾何何レノ方法ニヨルモ、又コレ等ヲ混用スルモ可ナリ。
5. 甲乙二個所ノ賣地アリ。其ノ面積ノ比ハ 7:6, 其一坪ノ提供價格ノ比ハ5:4 ナリトス。或ル人甲地ノ1/3、乙地ノ1/4ヲ一坪ニツキ提供價格ヨリ何レモ5圓ヅツ廉ク購ヒシニ買價ノ比ハ2:1ナリシトイフ。各地一坪ノ買價如何
一坪当たりの値引き前の価格を、甲地が 5x(円)、乙地が 4x(円)とおけば、
(7/3)・(5x-5) : (6/4)・(4x-5) = 2:1
となる。これを解けば、x=10 となることがわかる。よって、甲地の本来の価格は50円であり、乙地の本来の価格は40円となる。
まとめ
戦前のエリート校である旧制第一高等学校の数学の入試は意外と簡単だった。