本文
「治療法Aと治療法Bを偽薬を使った治療と比べてみた。治療法Aは偽薬に比べて有意な利点が見られたが、治療法Bは統計的に有意な利点がなかった。ゆえに治療法Aは治療法Bより優れている。」
こんな話が常にある。ここに述べられているように有意であるかないかの違いを見ることは、薬物治療、外科的処置、薬や手術によらない治療、そして実験結果を比較する簡単な方法だ。これは単純明快だ。そして、これは意味があることのように思える。
しかしながら、有意であるかないかの違いは、常に有意な差を生むわけではない [1] 。

セイウチの食事について比較する研究を考えてみよう。セイウチの1つのグループには普通の食事が与えられる。これに対して、他の2つのグループは新しく、より栄養のある食事が与えられる。1ヶ月後、研究者がセイウチの体重を量ったところ、栄養のある食事Aが与えられた場合は普通の食事が与えられた場合より25 kg 体重が重くなり、栄養のある食事Bが与えられた場合は普通の食事が与えられた場合より 10 kg しか体重が重くならなかったことが分かった。
各々の食事について平均してどれぐらい体重を増やすことが期待できるかについて立証したいとする。もし宇宙に存在する全てのセイウチにこれらの食事を与えたら、体重増加の平均はどうなるだろうか。今、手元にそんなに多くのセイウチはいないのだから、この問題に答えることは難しい。セイウチは一頭ごとにかなり違っていて、新しい食事以外の理由で体重を増やすことがありうる。(もしかしたら、オスのセイウチは水着の季節のために大きくなっているのかもしれない。)この違いを踏まえると、食事Bの効果は統計的に有意でないと算出される。10 kgの体重増加がこの食事によって引き起こされたと結論づけるには、セイウチ間の違いが大きすぎるのだ。しかし、食事Aは統計的に有意な体重増加を引き起こしており、おそらく有効であったのだろうと考えられる。
研究者は「食事Aは統計的に有意な体重増加を引き起こし、食事Bは引き起こさなかった。明らかに食事Aの方が食事Bより太らせている」と結論づけるかもしれない。他のセイウチの飼育者はこの論文を見て、食事Aの方がより効果的だから、体重不足の病気のセイウチに食事Aを与えようと決めるかもしれない。
しかし、本当にそうだろうか。必ずしもそうではない。
なぜならば、限られたデータしかないために、数値に内在的な誤差があるのだ。他の結果についてもどれがデータと矛盾しないかを計算することは可能だ。例えば、「本当」の食事Aの効果は35 kg の体重増加あるいは17 kg の体重増加かもしれず、セイウチの小さな標本において、そうした結果を見ることが十分にありうる。より多くのデータを集めることで、真の効果をより正確に突き止めることができよう。
統計には、この誤差を定量化するための手法がある。各々の測定の不確かさを計算した場合、両方の食事が全く同じ効果を持つということも十分にありうることが分かる。食事Bが体重を0 kg増加させることは全く十分にありえることなので、食事Bの効果は統計的に有意でない。しかし、食事Bが体重を20 kg増加させるのに、標本の中に含まれていたセイウチが異常に痩せていた可能性も十分にありうるのだ。同様に、食事Aも20 kgの体重増加をもたらし、研究の中で異常に食いしん坊のセイウチを使ってしまったということも全く十分にありえるのだ。より多くのデータがなければはっきりさせることができない。
食事Aと食事Bの間で統計的に有意な違いがあると結論づけるには、データが足りていない。片方の食事が統計的に有意な結果を出し、もう片方が出さなかったとしても、両者の間に統計的に有意な違いはない。両方とも同じぐらい有効かもしれない。2つの結果の有意性を比べるときは気をつけよう。もし2つの処置あるいは効果を比較したければ、両者を直接比較しよう。
普通の文献やニュースの中でこの種の誤りの例はたくさんある。例えば、神経科学の論文は、大きな割合でこの誤りを犯している [3] 。数年前に、男性は生物学的な兄 [4] が多いほど同性愛者となりやすいということを示唆する研究があったことを読者は覚えているかもしれない [5] 。どうやってこの結論に至ったのだろうか? そしてなぜ兄であって姉ではないのだろうか?
この論文の著者は、様々な要因とその同性愛への影響について分析を行うことで、結論について説明している。兄の数だけが統計的に有意な影響を示し、姉の数や非生物学的な兄の数は統計的に有意な影響を示さなかった。
しかし、今まで見てきたように、このことは兄の影響と姉の影響との間に統計的に有意な差が存在することを保証するものではない。実際、データを詳しく見てみると、兄の影響と姉の影響との間に統計的に有意な差は存在しないように見える。残念なことに、これを直接計算するに足るデータは、論文として公刊されていない [6] 。
有意差が見逃される時
この問題は他のところでも生じうる。科学者は以下のような図を用いて単に目で見るだけで有意差があるかを判断することを日常的に実施している。
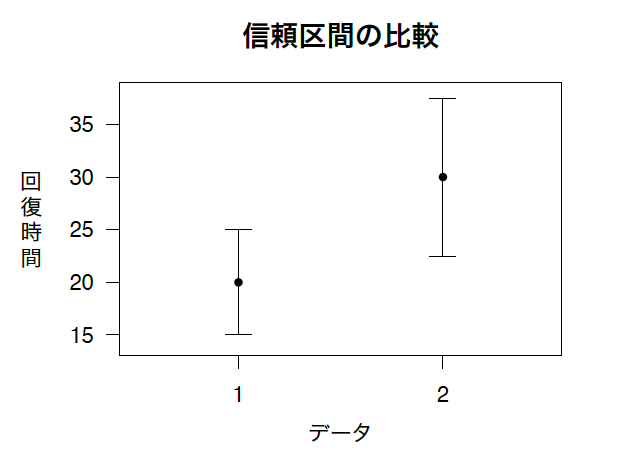
図中に描かれた2つの点が、各々10人の患者からなる2つの異なったグループでの、ある病気からの回復時間の推定を示しているものとしよう。図中のエラーバー [7] は3つの異なることを表しうる。
- 測定の標準偏差:各々の観察点がどれだけ平均から離れているかを計算し、その差を二乗し、その結果を平均して平方根を取る。これが標準偏差で、測定がどれだけ平均から散らばっているかを測るものだ。
- 何らかの推定量の標準誤差:例えば、エラーバーは平均の標準誤差を示すかもしれない。それぞれ別々の患者を含む標本がいくつもあり、それぞれの標本がちょうど$n$人の被験者を含むものとしよう。これらの標本を測定した場合、測定された平均回復時間の68%が、「真」の平均回復時間の標準誤差1個分の幅に収まるということが推測できる。(平均を推定する場合、標準誤差は、測定の標準偏差を測定の数の平方根で割ったものになる。だから、データを多く集めれば集めるほど、推定はより良くなる。しかし、推定が良くなるスピードはあまり早くない [8] 。)例えば最小二乗回帰のように、多くの統計的手法が、結果に対する標準誤差の推定を与える。
- 何らかの推定量の信頼区間:95%信頼区間とは、100個のランダムな標本の中から95のランダムな標本について真の値を含むように数学的に構成されたものである。だから、およそ各々の方向に大体標準誤差2つ分だけ広がっていることになる。(より複雑な統計モデルにおいては、これは正確でないかもしれないが。)
これら3種類は全て異なっている。標準偏差は自分のデータに対する単純な測定である。標準誤差は、平均や最も当てはまりの良い直線の傾きといった統計量について、患者の標本をいくつも取ったとしたら、どれぐらいの幅が見られるだろうかを教えてくれるものである。信頼区間は標準誤差に類似しているが、95%信頼区間の95%が「真」の値を含んでいるに違いないということを保証してくれる点で標準誤差と異なっている。
上述の図の例では、重なり合う2つの95%信頼区間がある。多くの科学者は、これを見て2つのグループの間に統計的に有意な差はないと結論づけるだろう。結局、グループ1とグループ2は違わないのかもしれない。平均回復時間は両方のグループで25かもしれない。そして、今回はグループ1が幸運であったために、違いが表れただけかもしれない。しかし、このことは差が統計的に有意であることを示すだろうか? $p$値はどうなるだろうか?
この場合、$p < 0.05$となる。たとえ、信頼区間が重なり合っていたとしても、グループの間には統計的に有意な差があるのだ [9] 。

残念なことに、多くの科学者は仮説検定を省き、信頼区間が重なっているかを確認するために、プロットをちらっと見るだけで済ましてしまう。これは実際には非常に保守的な検定である [11] 。信頼区間が重ならないように要求することは、状況によっては$p<0.01$を要求すること似たようなことになる [12] 。2つの測定の間に有意な差があるにもかかわらず、ないと主張するのは簡単なのだ。
逆に言えば、測定を標準誤差や標準偏差で比較することも誤解を招きやすい。標準誤差の幅は信頼区間の幅より狭いからだ。2つの観測結果で、標準誤差が重なり合わないが、両者の違いは統計的に有意でないことはありうるのだ。
心理学者・神経科学者・医学研究者に対する調査で、大多数の人がこの単純な過ちを犯していること、そして多くの科学者が標準誤差・標準偏差・信頼区間を混同していることが分かっている [13] 。気候科学の論文に対する他の調査では、2つのグループをエラーバーで比較している論文の大部分がこの過ちを犯していることを発見している [14] 。『誤差分析入門』といった実験科学者のための入門教科書でさえ、学生に対して目で見て判断するように教えており、正式な仮説検定を全くほとんど触れないでいる。
もちろん、目で見て比較できる信頼区間を生成する正式な統計手続きは存在する。その手続きは自動的に多重比較を修正してもくれる。例えば、ガブリエル比較区間 (Gabriel comparison interval) は目で見て簡単に解釈される [15] 。
信頼区間が重なっていることは、2つの値に有意差がないことを意味しない。同様に、標準誤差のバーが重なっていないことは、2つの値に有意差があることを意味しない。代わりに適切な仮説検定を用いることが常に最良の手段である。あなたの眼球はちゃんと定義された統計的手続きではないのだ。
この文章の続きは「停止規則と平均への回帰」を参照のこと。
- 原注:A. Gelman, H. Stern. The Difference Between “Significant” and “Not Significant” is not Itself Statistically Significant. The American Statistician, 60:328–331, 2006. [↩]
- 画像出典:Wikimedia Commonsよりパブリックドメイン画像を使用。 [↩]
- 原注:S. Nieuwenhuis, B. U. Forstmann, E. Wagenmakers. Erroneous analyses of interactions in neuroscience: a problem of significance. Nature Neuroscience, 14:1105–1109, 2011. [↩]
- 訳注:「生物学的な兄」とは要するに産みの親を同じにする兄のことである。 [↩]
- 原注:A. F. Bogaert. Biological versus nonbiological older brothers and men’s sexual orientation. PNAS, 103:10771–10774, 2006. [↩]
- 原注:A. Gelman, H. Stern. The Difference Between “Significant” and “Not Significant” is not Itself Statistically Significant. The American Statistician, 60:328–331, 2006. [↩]
- 訳注:図中で、各々の点を貫くように上下に伸びている線がエラーバーである。 [↩]
- 訳注:ここで、標準誤差の値が小さいほど、推定のぶれの幅が小さいということになる。標準誤差はデータの数の平方根の逆数に比例するので、データを2倍に増やしても、標準誤差の範囲は70.7%にしか狭まらない。データの数が3倍になっても57.7%、データの数が4倍で50.0%といったところだ。その意味で推定が良くなるスピードは「早くない」のである。 [↩]
- 原注:これは、グループ1の標準誤差は2.5、グループ2の標準誤差は3.5であるということに基づいて、対応なしの$t$検定で計算されたものである。 [↩]
- 画像出典:PixabayよりOpenClips氏のパブリックドメイン画像を使用。 [↩]
- 訳注:本文で述べられているように、通常、仮説検定と信頼区間だと、信頼区間の方がグループ間の差があると認定するハードルが高い。だが、これを逆から見れば、$p$が0.05より大きいか小さいかで判断する場合、仮説検定はグループ間に差があると認定する基準が緩すぎるという話になる。このため、$p$が0.05より大きいか小さいかという緩い基準で仮説検定は用いるべきではないと主張している人もいる。例えば、 V. E. Johnson. Revised standards for statistical evidence. PNAS, 110:19313–19317, 2013. を参照のこと。 [↩]
- 原注:N. Schenker, J. F. Gentleman. On judging the significance of differences by examining the overlap between confidence intervals. The American Statistician, 55:182–186, 2001. [↩]
- 原注:S. Belia, F. Fidler, J. Williams, G. Cumming. Researchers misunderstand confidence intervals and standard error bars. Psychological methods, 10:389–396, 2005. [↩]
- 原注:J. R. Lanzante. A cautionary note on the use of error bars. Journal of climate, 18:3699–3703, 2005. [↩]
- 原注:K. R. Gabriel. A simple method of multiple comparisons of means. Journal of the American Statistical Association, 73:724–729, 1978. [↩]