『データ解析のための統計モデリング入門』のレビュー

はじめに

『データ解析のための統計モデリング入門』という本を読んだので、その内容を簡単に紹介したい。この本では、一般化線型モデルと呼ばれる統計手法やその応用が紹介されており、R と WinBUGS というソフトが実際の解析に用いられている。

• 久保拓弥 (2012). 『データ解析のための統計モデリング入門―一般化線形モデル・階層ベイズモデル・MCMC』 東京：岩波書店．

この本は、全般的に説明があっさりとしている。このため、一般化線型モデルをしっかり学びたいのならば、（英語で書かれた）厚めの教科書を読んだ方が良いと私は思う。ただし、この本は、統計を使った学術研究がいかにいい加減なものであるか鋭く指摘している。この耳に痛い指摘は、統計を使って仕事をする人にとって一読の価値があると思う。

内容

副題にあるように、この本は、一般化線型モデル (GLM)、階層ベイズモデル、マルコフ連鎖モンテカルロ法 (MCMC) といった手法を扱っている。

モデルにするとは？

一般化線型モデルのような「モデル」といった言葉が耳慣れない人もいると思うので、これらの手法でどういうことができるのか簡単に説明しておこう。一般化線型モデルなどの手法を使うと、データに基づいて、現実世界の事象に対応する数理的なモデルを作ることができる。数理的なモデルがちゃんと作れれば、それに基づいて将来の予測 ^[1] などもできる。

具体的な例を通じてもう一度説明しよう。コムギの収量に関する問題を考える。コムギの収量は、栽培する地域によって変わってくるだろうし、コムギの品種によっても変化するだろう。また、日照条件、肥料、水はけなど、現実世界には収量に影響する様々な要因がある。こうした様々な要因をうまく組み入れてコムギの収量に関する数理的なモデルを作ることができれば、色々とうれしいことが起きる。例えば、肥料はどれだけ使えばよいのか、ある土地にはどの品種が適しているのかといったことが、この数理的なモデルから予測 ^[2] できる。一般化線型モデルや階層ベイズモデルというのは、こういった数理的なモデルの一種なのだ。

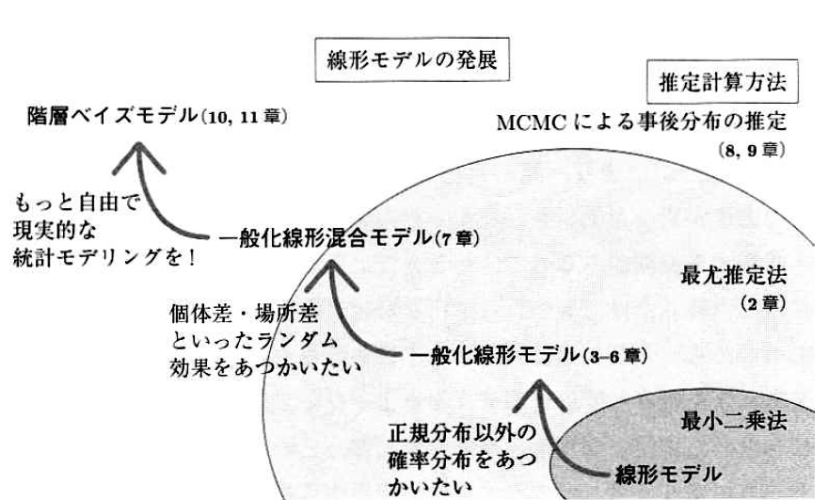
様々なモデルの関係は、この本のに載っている図 (p.6) が分かりやすいので、これを引用しておこう。左上にあるモデルほど応用的なものである。この図にあるように、一般化線形モデル→一般化線形混合モデル→階層ベイズモデルと、徐々に応用的なモデルに向かって進んでいく。応用的なモデルは難しいが、より適用範囲が広いモデルである。なお、モデルの関係の図の右下にある線形モデル ^[3] についてはこの本では扱われていない。線形モデル ^[4] はあくまでも一般化線形モデルの一部であるので、一般化線形モデルを説明した時点で説明し尽くしているのだ。

説明の流れ

さて、この本の内容の紹介に戻ろう。この本は以下の11章から成り立っている。各章の関係については、この本の冒頭に掲げられている「第2章以降の説明の流れ」の図が分かりやすいので、これをそのまま引用する。

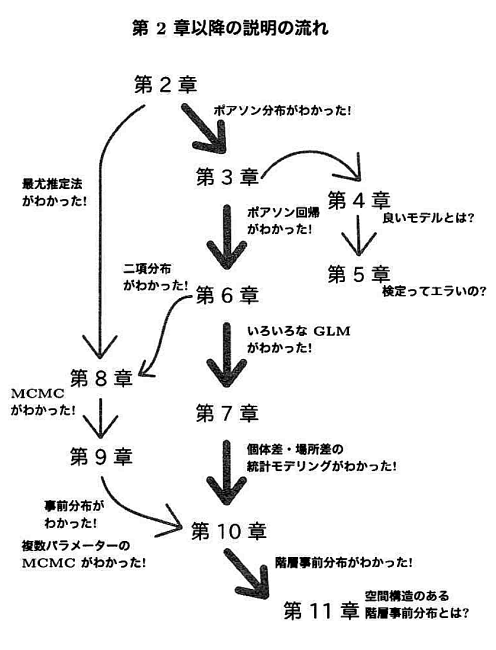
1. データを理解するために統計モデルを作る
2. 確率分布と統計モデルの最尤推定
3. 一般化線形モデル (GLM) ―ポアソン回帰―
4. GLMのモデル選択 ―AICとモデルの予測の良さ―
5. GLMの尤度比検定と検定の非対称性
6. GLMの応用範囲をひろげる ―ロジスティック回帰など―
7. 一般化線形混合モデル (GLMM) ―個体差のモデリング―
8. マルコフ連鎖モンテカルロ (MCMC) 法とベイズ統計モデル
9. GLMのベイズモデル化と事後分布の推定
10. 階層ベイズモデル ―GLMM のベイズモデル化―
11. 空間構造のある階層ベイズモデル

それでは、どのような内容が述べられているのか、章ごとに見ていきたいと思う。

モデルとは何か（第1章-第2章）

第1章の「データを理解するために統計モデルを作る」では、まず、モデルを立てるということはどういうことなのか説明している。その後、この本の説明の流れやこの本で登場する記号などについて触れている。

第2章の「確率分布と統計モデルの最尤推定」では、統計モデルというものはどういうものなのか、比較的簡単な例を通じて紹介している。具体的には、架空の植物の種子の数のデータに対して、ポアソン分布をモデルとして適用した例が挙げられている。そして、ポアソン分布とはどんな分布なのか、最尤推定 ^[5] とは何なのかということを説明している。さらに、統計モデルに関する全般的な話として、乱数発生・推定・予測とはどういうものなのか説明している。

一般化線形モデルとは何か（第3章-第6章）

第3章の「一般化線形モデル (GLM) ―ポアソン回帰―」では、いよいよ本題である一般化線形モデルの説明に入る。一般化線形モデルと言っても、実際には色々のものがあるのだが、ここではポアソン回帰という手法を中心に見ている。この章から得るべき教訓は、「何でも正規分布」や「何でも直線」で統計モデルを立てるのは無理があるということだ。

第4章の「GLMのモデル選択 ―AICとモデルの予測の良さ―」では、複数のモデルの中から「良い」モデルを選び出すためにはどうすれば良いかということを扱っている。「良い」モデルとは、あてはまりの良いモデルではなく、予測能力が高いモデルであるということが説明されている。そして、予測の良さを測る尺度として、AIC ^[6] を導入している。適当な教科書だと「AIC を使えば、モデルの良さを比較できます」と一言で終わってしまいがちであるが、この本ではなぜ AIC を使うとモデルの良さが比較できるのかをちゃんと説明している ^[7] 。このようにちゃんと説明してあるのは良かったと思う。

第5章の「GLMの尤度比検定と検定の非対称性」では、尤度比検定 ^[8] という手法が扱われている。ただ、尤度比検定に限らず、検定全般に関わる問題を説明した章と思って読んだ方が良いだろう。実際、著者自身もこの章の最後に、

と記している。

次に、第6章の「GLMの応用範囲をひろげる ―ロジスティック回帰など―」の内容について紹介しよう。先に第3章で GLM が導入されたが、その際はポアソン分布に基づく GLM しか見ていなかった。この第6章では、ポアソン分布だけでなく、二項分布・正規分布・ガンマ分布といった他の分布に基づく GLM の説明をしている。また、交互作用の話も少しだけ出てくる ^[9] 。この他の重要な指摘として、割算値 ^[10] を用いたモデルを作るのはやめるべき ^[11] ということが書かれている。

一般化線形モデルの拡張、そしてベイズへ（第7章-第11章）

第7章の「一般化線形混合モデル (GLMM) ―個体差のモデリング―」では、GLM の拡張として、GLMM を導入している。なぜ GLMM を導入するのかというと、観測されなかった個体差をモデルにうまく組み込むためである。

第8章の「マルコフ連鎖モンテカルロ (MCMC) 法とベイズ統計モデル」では、タイトルの通り、MCMC ^[12] とベイズ統計モデルの説明をしている。この章で扱う統計モデルは、前章までのモデルに比べ、さらに複雑になっている。私の個人的意見だが、MCMC にせよ、ベイズ統計モデルにせよ、かなり重い内容であるので、それぞれ独立して1章を立てた方が良かったと思う。2つの内容を1つの章にまとめたがために、足早な感が否めない。

第9章の「GLMのベイズモデル化と事後分布の推定」では、複数のパラメータを持つ GLM をベイズの枠組みに載せ、そこからベイズ統計モデルの事後分布を MCMC で推定する手法について紹介している。後は、MCMC サンプリング用のソフトウェアとして、WinBUGS を挙げ、その用法について簡単に説明している。

第10章の「階層ベイズモデル ―GLMM のベイズモデル化―」では、タイトルの通り、GLMMをベイズの枠組みに載せるとどうなるかを説明している。

さらに、第11章の「空間構造のある階層ベイズモデル」では、第10章の応用として、空間相関を含めたモデルをどう考えれば良いか紹介している。

説明の特徴

数学とか統計の本は硬い言葉遣いであることが多いが、この本は割合とゆるい文体で書かれている。本文はですます体である。なので、さらっと読む分には、すぐに読み終えることができると思う。

しかし、この本は、説明があっさりしているところは本当にあっさりしている。これは、枝葉末節を切り落として、統計モデルの作り方の根幹の部分だけを説明しようとしたためだろう。ただ、あっさりしすぎで物足りない部分も少なくない。そもそも、この本は270ページぐらいしかない。決して薄くはないが、一般化線型モデルから階層ベイズモデルまで内容が盛りだくさんなので、やはりどうしてもこの1冊では足りないのだろう。要するに、内容に紙幅が追いついていないのである。この本は、最初の方が説明が丁寧である。これに対し、後半（第7章以降）は詰め込みすぎで、重要な事項がさらっと流されている感がある。

だから、この分野のことをちゃんと勉強したい人は他の本を読むと良い ^[13] 。少なくとも私はそう思う。例えば、以下の Dobson & Barnett (2008) が良いだろう ^[14] 。

• Dobson, A. J. & Barnett, A. G. (2008). An Introduction to Generalized Linear Models, Third Edition. Boca Raton, FL: CRC Press.

そうなると、『データ解析のための統計モデリング入門』を読む意味がないように思われるかもしれない。とは言え、この本は GLM などの手法がどのようなことをしているのか大まかにつかむ際には便利だ。先に述べたように、さらっと読む分にはすぐ読み終えることができるのだ。ただし、重ねて言うが、「この本だけで GLM を使いこなせるようになりました！」という本ではない。上に挙げた Dobson & Barnett (2008) のような教科書を読みつつ、もっとしっかりと学ばないと身につかないと私は思う。

ブラックボックス統計学批判

思うに、この本の面白さは、いい加減な統計の使い方を批判しているところにある。世の中には、統計をいい加減に使って研究している人が多いのだが、この本はこうした人たちをばっさり切っている。例えば、この本の1.2節で、著者はデータ解析で「理解しないままソフトウェアを使う」作法をブラックボックス統計学と呼び、これは擬似科学の作法であると指摘している。

「研究の時に使う手法って当然ちゃんと知っているものでしょう？」と思う人もいるかもしれない。だが、手法が分からないまま研究している学者は意外に多い。そういう学者はどうしているのかというと、データをSPSSやら何やらの統計ソフトに入れて出てきた「結果」をそのまま使うのである。入力したデータと出力された「結果」の間に何が起こったか分かっていないわけである。つまり、こうした学者にとっては、入力と出力の間がブラックボックスなのである。

この本の著者は生態学が専門なのだが、生態学研究においてはこのようなブラックボックス統計学がはびこっていたらしい。この本の行間からも、ブラックボックス統計学打破のために著者が努力してきた影がうかがわれる。

ブラックボックス統計学の問題の核心を突いた言葉を以下に引用しよう。この言葉は、この本で最も重要な指摘であると私は思う。

これはかなり鮮烈な批判である。こうしたブラックボックス統計学に対する批判が読める点が、この本の良いところだと思う。また、実際にこの本ではブラックボックス統計学の異常な点をいくつも指摘している。先に各章の内容を紹介したときにも述べたが、例えば第5章で検定の濫用を問題として挙げている。

というわけで、この本は、GLM などを学びたいという人が読むよりも、日頃ブラックボックス統計学に悩まされている人が読んだ方が面白いかもしれないというのが、私の感想である。なお、ここで言われている内輪の「秘儀」の問題について私の思うところを書いたので、興味がある方はお読みいただければ幸いである。

1. 数理的なモデルを作らなくても予測はできるが、数理的なモデルの方が取り扱いやすいだろう。 [↩]
2. 魔法の鍵のように、何でもかんでも予測できるわけではない。 [↩]
3. この線形モデルは、一般線形モデル (general linear model) とも呼ばれる。一般化線形モデル (generalized linear model) と名前が紛らわしいので注意。 [↩]
4. よく耳にする「分散分析」や「単回帰分析」とかは、この狭義の線形モデルで扱われる内容である。 [↩]
5. 単純化して言えば、最尤推定とは一番あてはまりの良いパラメータを探す手法のことである。 [↩]
6. AIC とは、Akaike’s Information Criterionの略である。日本語にすると赤池情報量規準。 [↩]
7. もっとも、この本では、数理統計学的に AIC を導出することまではしていない。それよりも、どういう考えに基づいているのかということを言葉で説明している。 [↩]
8. 尤度比検定は、複数のモデルを比較考量する手法の1つである。 [↩]
9. ただし、この本は交互作用の話は本当に少ししかしていない。 [↩]
10. 割算値の例として、野球の打率がある。打率は、安打数を打数で「割る」と出てくる値である。1000打数300安打と10打数3安打は、打率にすると3割ということで全く同じになってしまう。こういった場合は、打率をモデルに組み込む代わりに、打数と安打をモデルに組み込むとうまくいくのである。 [↩]
11. 割算値に限らず、観測値をこねくりまわしてつくった指標の使用も避けるべきである。 [↩]
12. この本では、MCMC アルゴリズムの1つとしてメトロポリス法を紹介している。 [↩]
13. 実際、『データ解析のための統計モデリング入門』の各章の最後には、この本で扱えきれなかったことを扱っている書籍が色々挙げられている。著者としても、詳しいことは他の本を読んでもらいたいということなのだろう。 [↩]
14. 実は、『データ解析のための統計モデリング入門』の第3章の最後でも、Dobson & Barnett (2008) が推薦されている。 [↩]