はじめに
統計分析をする際には、グラフを描くことがしばしば行われる。しかし、そもそも、なぜグラフを描く必要があるのだろうか。グラフを描く理由には、大きく分けて分析と伝達という2 つの側面がある。分析のためというのは、複雑なデータから何か物事を発見するためにグラフを描くことである。これに対して、伝達のためというのは、データの内容を他の人に分かりやすく伝えるためにグラフを描くことである。決して、レポートや論文のページ数を埋めるためにグラフを描くのではない。
グラフは統計分析において有用な手立てである。それにも関わらず、検定や推定といった複雑な計算を伴うような統計的手法の方が、グラフを描くことよりも優れた手法であると思い込んでいる人も少なくない。しかし、グラフをうまく使うと、複雑な計算を経ても分からないことがいとも簡単に分かることすらある。
グラフに対する偏見
1973年に、フランシス・アンスコムという人が、統計分析におけるグラフについて論じた以下の論文を書いた。
- Anscombe, F. J. (1973). Graphs in Statistical Analysis. American Statistician, 27(1), 17–21.
この論文の中で、アンスコムは、以下のような考えに毒されていない人はほとんどいないと述べている。
- 数値的計算はきっちりとしたものであるのに対し、グラフは大まかなものだ。
- どのような統計データにも唯一の正しい統計分析手法がある。
- 複雑な統計的計算をした方が実直で、実際にデータを見るのはごまかしである。
アンスコムが指摘したこれらの間違った見方は、今でもまだ存在する誤解である。最近、ある人が私に統計的手法について質問することがあった。私はその時「それは状況によって使うべき手法が異なる」と答えたのだが、その質問した人は私の答えに納得していないようであった。この質問をした人は、上の2番に挙げたように、どのような統計データにも唯一の正しい統計分析手法があると思っていたのであろう。
何はともあれ、複雑な計算の方が重視され、グラフは軽視されがちであるが、それはよろしくない。グラフを有効に使えば、よりよい統計分析が行えるのである。
なお、アンスコムは、上述の論文でグラフの目的として以下のようなものを挙げている。
- データの大まかな特徴を知る
- 大まかな特徴の裏にあるものを知る
また、検定などの統計の計算は、何らかの仮定に基づくものが多いが、その仮定の正否を確かめる際に、グラフは有用であるともアンスコムは述べている。
グラフを用いることで分かる違い
統計分析に当たって、平均や相関係数を求めるといった計算はしばしば行われる。だが、こういった計算では捨象されてしまうことが、グラフを用いることで違いが分かることがある。これこそが、統計分析におけるグラフの有用性の1つである。
データの分布と平均
何かデータが与えられたとき、とりあえず平均を求めることはしばしば行われる。統計分析に慣れていない人は、単に平均だけ求めてそれで良いとしてしまうことが多い。だが、平均というのは、データの色々な側面を1つの数値に圧縮したものなので、それだけではデータの本質を見失ってしまうことがある。
以下の図を見てもらいたい。
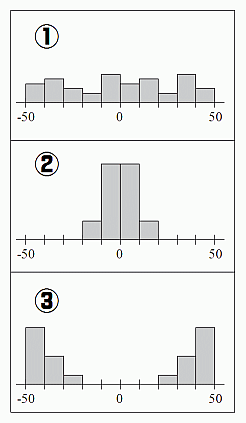
上の図で、①から③まで平均はすべて0である。単に、平均だけしか見ないと、①から③はまったく同じということになる。しかし、グラフを見れば一目瞭然であるが、①から③はデータの分布がまったく異なっている。①は広く薄くデータが散らばっているのに対し、②はデータが中央に集中している。③はデータが両極端に分かれている。
単に平均しか見なかった時には覆い隠されていたことが、グラフを描くことで分かったのである。
同じ回帰直線、異なった状況
以下に述べるのは、先に挙げたアンスコムの1973年の論文に挙げられていた例である。
統計分析では、2変数の関係を示すために、回帰直線を引くということがしばしば行われる。下に挙げる図では、まったく異なった状況に対し、まったく同じ回帰直線が引かれている。
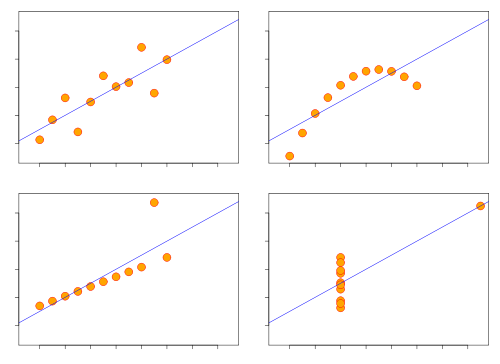
全然違った状況なのに、同じ回帰直線を引くのは変だと思う人もいるだろう。だが、普通に回帰直線を引くと、上図のようにまったく同じものになってしまうのである。
もしも、回帰直線の数式を求めるだけで、データを図示することを行わなければ、上記の図の4つの状況はまったく同じものだと誤解してしまうのである。ここからも、ちゃんとグラフを描くことの有用性が分かるだろう。