【翻訳】ダメな統計学 (7) 停止規則と平均への回帰

本文

医学に関する試験は多額の費用を要する。たくさんの患者に対し、実験的な薬物治療を実施し、何ヶ月もの間、その症状を追跡することは、相当な量の資源を消費する。このため、多くの製薬会社が「停止規則」(stopping rule) を発達させてきた。これは実験的な薬が実質的な効果を持つと明らかになった場合、調査者が研究を早めに終えることを許す規則である。例えば、試験は半分しか終わっていないものの、新しい薬について、症状に統計的に有意な差がすでに存在するならば、研究者は結論をより強固なものにするためにより多くのデータを集めるのではなく、研究を終わらせてもよい。

しかし、下手に行われれば、このことは偽陽性を多数もたらしてしまう可能性がある。

例えば、2つのグループの患者を比較するとしよう。ただし、一方のグループには薬が投与され、もう一方のグループには偽薬が投与されるものとする。薬が働いているかを調べるために、あるタンパク質について血流中での濃度を測定する。ただ、ここで、この薬は全く違いをもたらさない。もちろん、人によって濃度は少し異なるだろうが、2つのグループで、患者のタンパク質の濃度の平均は同様である。

各々のグループについて10人の患者から始め、徐々に、より多くの患者からより多くのデータを集めるものとする。進める際に、2つのグループを比較するために$t$検定を行い、平均のタンパク質濃度の間に統計的な有意差があるかを見る。このシミュレーションのような結果が得られることになるだろう。

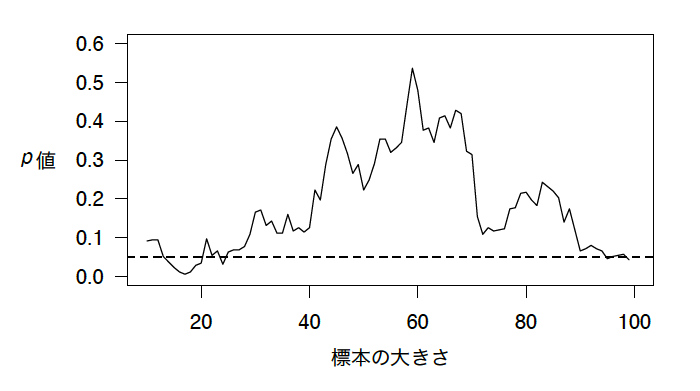
この図は、より多くのデータを集めたときのグループ間の差異についての$p$値を示している。水平線は$p = 0.05$の有意水準を示している ^[1] 。最初は、有意差がないように見える。そして、より多くのデータを集めて、有意差があると結論づける。もし中止したとしたら、誤ったことを信じていただろう。グループ間の有意差が本当は存在しないにもかかわらず、有意差があると信じていただろう。さらに多くのデータを集めたら、間違っていたということに気づく。結局、ちょっとした幸運が偽陽性へと導いてしまっていたのだ。

グループの間で本当の違いがないのだから、$p$値が一時的に小さくなることが起きるわけがないと思うかもしれない。つまり、より多くのデータを取ることで、結論をよりダメなものにしてしまうわけがないというわけだ。そうだよね？ 再度試験を行った場合、最初からグループ間に有意差がなく、より多くのデータを集めてもそのまま有意差がないままでいるというのはありえる。また、巨大な差が存在する状態で始まり、即座に差がない状態に戻るというのもありえる。しかし、もし充分長く待ちつつ、データポイントが1つ加わるごとに検定するならば、たとえ本当は差が全くなくても、任意の値の統計的有意水準を下回ることがあるだろう。通常、無限の標本を集めることはできないので、現実にはこうしたことが常に起きるわけではないが、そうだとしても、うまく実施されない停止規則は偽陽性率を大きく上昇させる ^[2] 。

現代の臨床試験では、統計に関する実験計画をあらかじめ登録することがしばしば求められる。そして、一般的には、観察1つが終わったらそのつど検定するのではなく、証拠を検定するための少数の評価点を先に選んでおく。このことは偽陽性率を少ししか引き上げず、しかもここでの偽陽性率は、必要な有意水準を注意深く選び、より進んだ統計的技法を用いることで調整することができる ^[3] 。しかし、実験計画が登録されず、研究者が適切だと感じる手法を何でも使える自由がある分野では、偽陽性の悪魔が潜んでいるかもしれない ^[4] 。

真実の誇張

医学に関する試験は、薬の間の中程度の差異を検出するための検定力が十分でない傾向にもある。だから、効果を見つけたらすぐにやめたくとも、効果を検出するのに十分な検定力がないのだ。

ある薬が、偽薬に比べて20%症状を減らすとしよう。しかし、検定するために実施している試験は、この差異を検出するための十分な検定力がないものとしよう。小規模の試験では、幅広い結果が出る傾向があることが知られている。普通より短いかぜをひいている10人の幸運な患者を得ることは簡単だが、みんな普通より短いかぜをひいている1万人を得ることは、ずっと難しいのだ。

この試験を何回も実施することを想像してみよう。時には不幸な患者を得て、薬から得られる統計的に有意な改善に気づかないこともある。時には患者がちょうど平均的で、実験群では症状が20%減少する——だが、これを統計的に有意な増大と呼ぶには十分なデータがないので、これを無視する。時には患者が幸運で、症状が20%よりずっと多く減少する。そして、試験を止めて、「ね！ うまくいっただろ！」と言うことになる。

薬が有効であると正しく結論づけることができたが、その効果の大きさを誇張してしまった。この薬が実際よりもずっと有効であると誤って信じてしまったのである。

こうした現象は、薬物試験、疫学研究、遺伝子関連解析（「遺伝子Aが状況Bを引き起こす」）、心理学研究、そして医学文献の中で最も良く引用されている論文で発生している ^[5] 。（遺伝子関連解析のように）多くの独立した研究者によって試験が短時間で行われる分野では、最も初期に公刊される結果はしばしばきわめて矛盾したものとなる。小規模試験と統計的有意性を求めることとによって、最も極端な結果しか公刊されないことになるからだ ^[6] 。

おまけに、真実の誇張は早期停止規則によって引き起こされうる。もし臨床試験でほとんどの薬が、試験を早期に止めることを保証できるほど有効でない場合、早期に停止される試験の多くは、幸運な患者と大したことのない薬の結果ということになるだろう。そして、試験を停止することは、差を判断するのに必要な追加のデータを自身から奪っていることになる。早期に停止した試験と、同じ課題に取り組んで早期に停止しなかった他の試験とを比べた報告がある。この報告によると、ほとんどの場合、早期に停止した試験は、試験対象となった治療の効果を誇張しており、その誇張の度合いは平均して29%であった ^[7] 。

もちろん、研究対象となっているいかなる薬についても「真実」は知りようがない。だから、早期に停止した研究が、幸運によるものなのか特に良い薬によるものなのかを判断することはできない。多くの研究は、元々意図していた標本の大きさ (sample size) や研究を終わらせることを正当化するために用いられた停止規則さえ公表しようとしない ^[8] 。試験が早期に止められていることは、その結果が偏っていることを自動的に示す証拠ではない。しかし、偏っていることをほのめかすものである。

小さな極端なもの

あなたが公立学校の改革を担当しているとしよう。最も良い教授方法についての調査の一部として、あなたは、学校の大きさが標準化されたテストの得点に与える影響を見ている。小さい学校の方が大きい学校よりうまくいっているのだろうか？ あなたは小さな学校をたくさん建てるべきだろうか？　それとも大きな学校を少しだけ建てるべきだろうか？

この問題に答えるため、成績上位の学校のリストを集めた。平均的な学校には千人程度の生徒がいるが、成績上位の5校あるいは10校はほとんどすべてそれより生徒の数が少なかった。このことは、小さい学校が最も良くやっているように見える。もしかしたら、教師が生徒を知ることができて、個別に助けることができる個人的な雰囲気によるものかもしれない。

そして、あなたは、成績下位の学校は何千人もの生徒と働きすぎの教師がいる都会の大きな学校だろうと予測しつつ、成績下位の学校を見てみた。なんと！ 成績下位の学校もみんな小さな学校だった。

何が起きているのだろうか？ テスト得点と学校規模の関係を示した図を見てみよう。

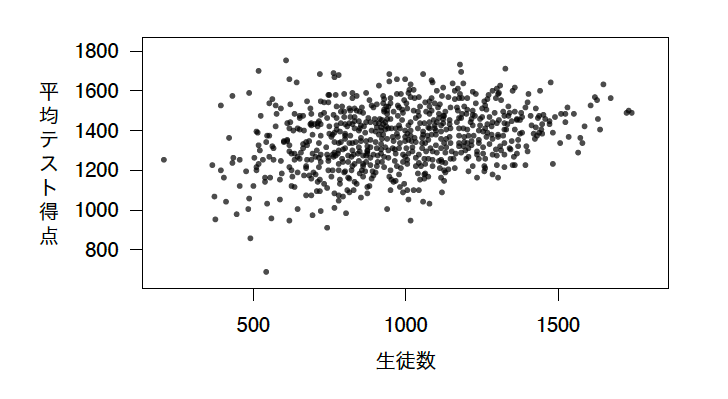
学校の中でも小規模なものほど、テストの平均得点が大きくばらついている ^[9] 。これは、こうした学校に生徒が少ないために散らばっているのに他ならない。生徒が少なければ、教師の「真」の能力をはっきりさせるデータ点 ^[10] が少ないということになる。だから、平均得点は大きくばらつくのだ ^[11] 。学校が多くなるほど、テスト得点のばらつきは少なくなる。そして、実は平均してテスト得点は増加しているのだ。

この例はシミュレーションで作られたデータを用いている。しかし、この例は、ペンシルベニアの公立学校の実際の（そして驚くべき）観察結果に基づいて作られたものである ^[12] 。

他の例を挙げよう。アメリカでは、腎臓ガン罹患率の最も低い部類の郡は、中西部・南部・西部の田舎の郡である傾向がある。どうしてこうなるのだろうか？ 様々な説明を考えることができるだろう。田舎の人は、運動量が多く、汚染の少ない空気を吸い、そしてもしかしたらストレスの少ない生活をしているのかもしれない。こうした要因がガン罹患率を下げているかもしれない。

これに対して、腎臓ガン罹患率が最も高い部類の郡は、中西部・南部・西部の田舎の郡である傾向がある。

もちろん、田舎の郡が人口がとても少ないことに問題のカギがある。10人の住民しかいない郡 ^[13] で、腎臓ガン患者が1人いれば、その郡が国内でもっとも腎臓ガンが高い郡となってしまう。つまり、小さな郡は、単に住民が非常に少ないために、腎臓ガン罹患率が非常にばらつくのである ^[14] 。

1. 訳注：この水平線より下に来ていれば、$p < 0.05$となり、有意差があると結論づけてしまう。 [↩]
2. 原注：J. P. Simmons, L. D. Nelson, U. Simonsohn. False-Positive Psychology: Undisclosed Flexibility in Data Collection and Analysis Allows Presenting Anything as Significant. Psychological Science, 22:1359–1366, 2011. [↩]
3. 原注：S. Todd, A. Whitehead, N. Stallard, J. Whitehead. Interim analyses and sequential designs in phase III studies. British Journal of Clinical Pharmacology, 51:394–399, 2001. [↩]
4. 訳注：ベイズ統計の手法に逐次確率比検定というものがある。この手法は、データを増やすたびに検定を行う手法であるが、普通の検定と違って、(1) 有意差があると結論づける、(2) 有意差がないと結論づけるという2つの選択肢の他に、(3) 判断を留保してもっとデータを集めるという選択肢が用意されている。このため、本文で述べられたような問題が起こりにくくなっている。 [↩]
5. 原注：J. P. A. Ioannidis. Why Most Discovered True Associations Are Inflated. Epidemiology, 19:640–648, 2008.
   J. P. A. Ioannidis. Contradicted and initially stronger effects in highly cited clinical research. JAMA, 294:218–228, 2005. [↩]
6. 原注：J. P. A. Ioannidis, T. A. Trikalinos. Early extreme contradictory estimates may appear in published research: the Proteus phenomenon in molecular genetics research and randomized trials. Journal of Clinical Epidemiology, 58:543–549, 2005. [↩]
7. 原注：D. Bassler, M. Briel, V. M. Montori, M. Lane, P. Glasziou, Q. Zhou, D. Heels-Ansdell, S. D. Walter, G. H. Guyatt. Stopping Randomized Trials Early for Benefit and Estimation of Treatment Effects: Systematic Review and Meta-regression Analysis. JAMA, 303:1180–1187, 2010. [↩]
8. 原注：V. M. Montori, P. J. Devereaux, N. Adhikari. Randomized trials stopped early for benefit: a systematic review. JAMA, 294:2203–2209, 2005. [↩]
9. 訳注：図の左側の方に表されているのが小規模の学校である。小規模の学校のテスト得点は上から下までばらついている。これに対して、図の右側の方に表されている大規模の学校は、テスト得点がそれほど上下にばらついていない。 [↩]
10. 訳注：個々の生徒の得点は、それぞれが教師の教える能力を反映したデータ点として捉えることができる。 [↩]
11. 訳注：これは今まで触れてきた薬の効果の試験と全く同じ話である。薬について調べる際、わずかな数の患者に対してしかデータを取らなかった場合のことを思い出してみよう。例えば、10人しか患者がいなければ、薬が効果を及ぼさない場合でも、全員がたまたま軽い症状だったという可能性は低くない。逆に全員がたまたま重い症状だったという可能性も低くない。つまり、人数が少ないと、極端な結果が出やすい。もし1万人の患者がいれば全員がたまたま症状が軽かったり重かったりすることは少ないだろう。つまり、人数が多いと、極端な結果が出にくくなる。学校の生徒の人数とテスト得点の話も、この薬の試験の話と同じである。人数が少ない方が極端な結果が出やすく、多い方が出にくいのである。 [↩]
12. 原注：H. Wainer. The Most Dangerous Equation. American Scientist, 95:249–256, 2007. [↩]
13. 訳注：アメリカの郡 (county) は大きいものから小さいものまで様々あるが、さすがに10人しか住民のいない小さな郡はない。ただし、数百人しか住人がいない小さな郡ならば多数存在する。なお、アメリカにはおよそ3,000の郡があり、1郡の住民数は平均10万人程度である。 [↩]
14. 原注：A. Gelman, P. Price. All maps of parameter estimates are misleading. Statistics in Medicine, 18:3221–3234, 1999. [↩]