本文
単に十分なデータを取らないだけで、実際に存在する効果を見つけられない可能性があることを見てきた。ほとんどの場合、これは問題となる。うまくいきそうな薬を見つけられなかったり、重大な副作用に気づかなかったりするかもしれない。データをどれだけ集めれば良いかということは、どうすれば分かるだろうか。
統計学者は「検定力」(statistical power) [1] という形で答えを用意している。ある研究における検定力とは、単なる幸運からある程度の大きさのある効果を区別する可能性のことを指す。薬から得られる大きな利益は簡単に検出できるだろうが、微妙な違いを検出することはずっと可能性が低い。簡単な例を見てみよう。
ギャンブラーが、相手が不正なコインを持っていると確信しているとしよう。このコインは、表と裏が出る割合が半々ではなく、出る割合が違っている。そして、相手は非常に退屈なコイン投げゲームで不正をするためにこのコインを使っている。このことをどう確かめれば良いだろうか?
単にコインを100回投げて、表が出た回数を数えるのではだめだ。たとえ、完全に公正なコインであったとしても、いつも50回表が出るわけではない。
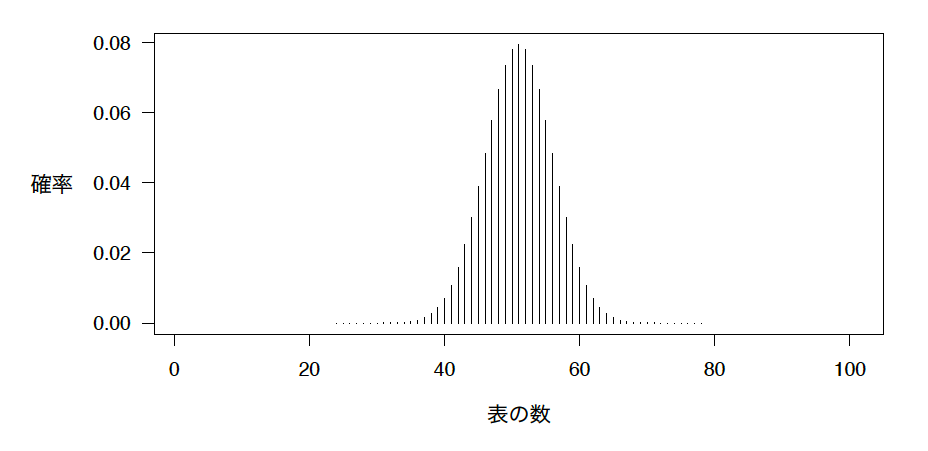
これは、100回コインを投げたときに、表が何回出るかという可能性を示したものである。
50回表が出る可能性が一番高いことが分かるが、45回表が出たり、57回表が出たりする可能性もかなり高い。だから、57回表が出たとしたら、コインは不正なものだったかもしれないが、単に運がよかっただけかもしれない。
数学的に解いてみよう。例えば、科学者がよくするように、$p$値が0.05以下になるところを探そう。つまり、10回または100回の試行の後に、表の出た数を合算し、表が半分で裏が半分になるだろうという期待からのずれを求める。公正なコインではそれ以上のずれが起きる可能性が5%しかなければ、コインが不正なものだということにしよう。そうでなければ、何も結論づけることはできない。コインは公正かもしれないし、少し不正かもしれない。判断が付けられないのだ。
さて、もし10回コインを投げて、上記の基準を適用したとしたら、どうなるだろうか。
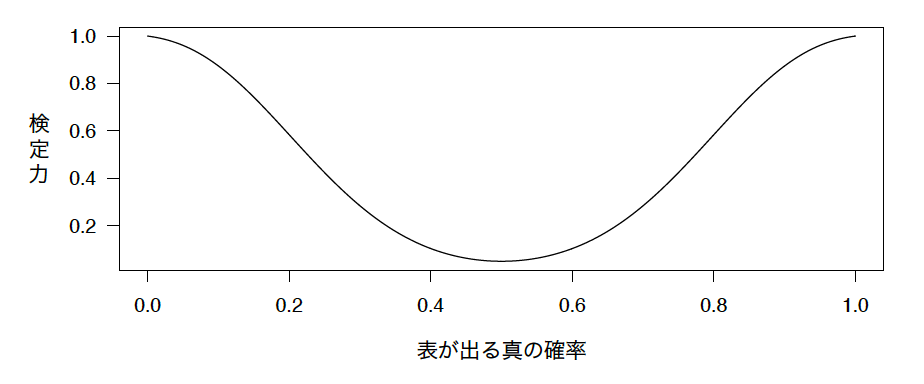
これは検定力曲線と呼ばれるものだ。横軸にそって、コインの表が出る真の確率ごとに異なった可能性が示されている。コインの表が出る真の確率は不正さの度合いに対応している。縦軸は、10回投げたあと、その結果に対する$p$値をもとに、コインに不正があると結論づける確率だ [2] 。
コインが不正なもので60%の確率で表が出るものであるとき、10回投げた場合、不正があると結論づけられる確率は20%しかない。データが少なすぎて、無作為な変動から不正を区別することができないのだ。不正に必ず気づくためには、コインが信じられないほど偏ってなくてはならない。
しかし、もし100回コインを投げたとしたら?
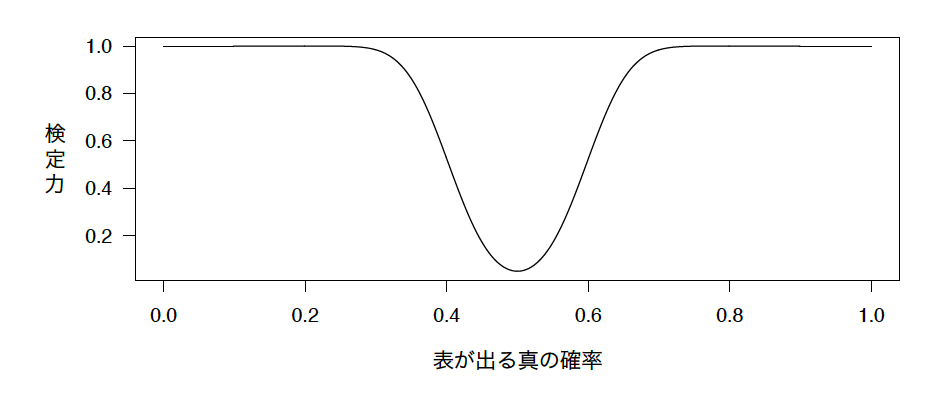
あるいは1000回ならば?
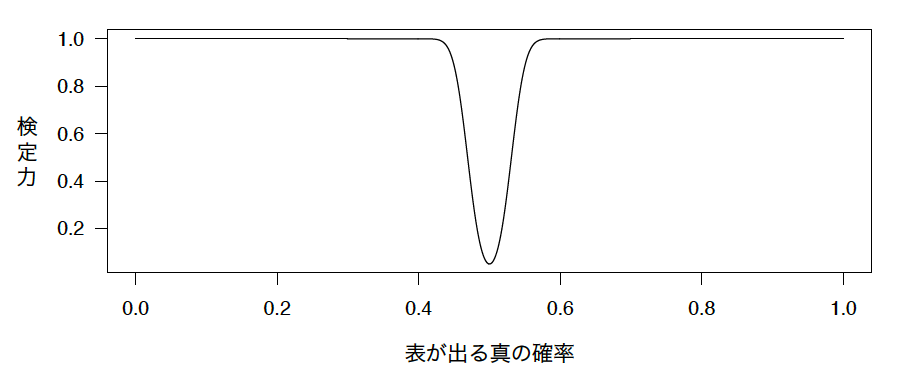
1000回投げれば、コインに不正があって60%表が出るということを簡単に判断することができる。公正なコインを1000回投げて、600回以上表が出ることは、ほとんどありえないからだ。
足りない検定力
こうしたことを聞けば、検定力の計算が、医学に関する試験において必要不可欠であると考えるかもしれない。科学者は、新しい薬が生存率を10%以上改善するかを試験するためにどれだけの患者が必要なのかについて、知りたいかもしれない。検定力を手っ取り早く計算することでその答えが得られるだろう。一般に、科学者は検定力が0.8以上であれば満足する。これは、実際の影響があると結論づける確率が80%であることに対応する。
しかし、この計算をする科学者はほとんどいないし、学術誌の記事で検定力を報告する記事もほとんどない。
同じ条件の下で、2つの異なった薬を与える治療を試すことを考えてみよう。どちらの薬がより安全なのか知りたいところなのだが、あいにくどちらの薬も副作用がまれであるとする。各々の薬は100人の患者に対して試験できるものの、各グループで深刻な副作用が生じるのはほんの少ししかないものとする。
明らかに、副作用の割合を比較するために十分なデータがない。もし片方のグループで4人に深刻な副作用が生じ、もう片方のグループで3人に深刻な副作用が生じたとしたら、その違いが薬のせいかどうか判断できないのだ。
不幸なことに、十分なデータがないためにきわめて大きな違い以外は検出できないということに言及せずに、「有害な影響に関して、グループの間に統計的に有意な差がない」という結論をしている試験はたくさんある [3] 。そして、そのために、片方はもう片方よりずっと危険かもしれないのに、医師が2つの薬は同じぐらい安全だと誤って考えてしまうのだ。
これは、弱い効果しか持たない薬に関する問題でしかないと思うかもしれない。しかし、違うのだ。1975年から1990年までの間に権威ある医学誌に公刊された研究から抽出されたある標本では、ランダム化比較試験 [4] の27%が否定的な結果 [5] を示していたのだが、そのうち64%が、グループの間の主要評価項目の50%の違いを明らかにするのに十分なデータを使っていなかったのだ。50%! たとえ、ある薬が他の薬に比べて症状を50%減らすとしても、その薬がより効果的だと結論づけるために十分なデータがないのだ。そして、否定的な結果を示した試験の84%が、25%の差を発見する検定力がなかったのだ [6] 。
神経科学では、問題はもっと悲惨だ。ある特定の効果を調べているたくさんの神経科学の論文から集められたデータを合算して、効果量について強い推定量が出てきたとしよう。合算対象となっている個々の研究のうち、中央値にあたる研究がこの効果を検出できる可能性は20%しかない。たくさんの研究を合算してはじめて効果を発見できるのだ。同様な問題は、実験動物を使う神経科学の研究でも起きており、大きな倫理的問題を引き起こしている。もし、個々の研究の検定力が足りなければ、本当の効果は多くの動物を使ったたくさんの研究が終了して解析されてからでないと本当の効果は発見されないだろう。最初にちゃんと研究が行われるよりずっと多くの実験動物を使うのだ [7] [8] 。
これは科学者がグループ間で有意な差がないと述べているとき、科学者が嘘をついていると言うものではない。実際の違いがないことを意味すると誤解してしまっているだけだ。違いがあるかもしれないが、研究の規模が小さすぎて違いに気づくことができないのだ。
日常的な例を考えてみよう。
赤信号での誤った方向転換
1970年代、アメリカの多くの地域で、赤信号で車が右折することが許されるようになった。それに先立つ長い間、道路の設計者と土木技師は赤信号での右折を許すと衝突や歩行者の死亡が増えるので危険であると主張してきた。しかし、1973年の石油危機とその影響により、通勤する人が赤信号を待って燃料を無駄にするしないように、赤信号で右折することを許すべきだと政治家が考えるようになった。
この変化が安全に対して与える影響を考察するためにいくつかの研究が行われた。例えば、バージニアの高速道路および交通部門のコンサルタントは、赤信号でも右折が許されるようになった20箇所の交差点で、変化前と変化後の違いを調べる研究をした。変化前は、これらの交差点で事故が308回あった。変化後は、同様の長さの期間で事故が337回あった。しかし、この差は統計的に有意でなかったため、コンサルタントは安全に対する影響がないとの結論を出した。
これに続くいくつかの研究も同じような結果だった。すなわち、衝突回数は少し増加するが、その増加量が統計的に有意であると結論するには十分なデータがないということだ。ある報告は以下のような結論を述べている。
(赤信号での右折の)採用以降、右折が関わる歩行者事故が増加したと疑う理由はない……
このデータに基づいて、さらに多くの市や州が赤信号での右折を許すようになった。もちろん、問題はこれらの研究が検定力が足りないことである。車にひかれる歩行者が増え、衝突に巻き込まれる車も増えたのだが、このことを確信をもって示すための十分なデータを誰も集めることができなかった。数年後、衝突と歩行者の事故が有意に増加している(時には100%近くの増加もあった)という明確な結果がもたらされるまでは [9] 。検定力の足りなかった研究に対する誤った解釈が命を奪ったのである。
この文章の続きは「擬似反復:データを賢く選べ」を参照のこと。
- 「検定力」は「検出力」または「統計力」と呼ばれることもある。 [↩]
- 訳注:10回投げて得られた結果に対して、二項検定と呼ばれる検定を行い、$p$値を求める。ここで、$p < 0.05$ならば、コインに不正があると結論づけることになる。 [↩]
- 原注:R. Tsang, L. Colley, L. D. Lynd. Inadequate statistical power to detect clinically significant differences in adverse event rates in randomized controlled trials. Journal of Clinical Epidemiology, 62:609–616, 2009. [↩]
- 訳注:ランダム化比較試験 (randomized controlled trial; RCT) とは、主に医学の分野で使われる科学実験の実験デザインの1つである。このデザインでは、効果を調べたい治療法を施すグループ(実験群)とそれと比較するためのグループ(対照群)を設けて、効果がどれだけあるかを調べる。また、被験者を偏りなく選び出した上で、偏りなく実験群と対照群に割り当てを行うこともこの実験デザインの重要な特徴である。 [↩]
- 訳注:2つのグループの違いを比べようと実験を行った場合、2つのグループの間に明確な差が見いだせない場合がある。否定的な結果 (negative result) とは、そういった場合のことを指す。 [↩]
- 原注:D. Moher, C. S. Dulberg, G. A. Wells. Statistical power, sample size, and their reporting in randomized controlled trials. JAMA, 272:122-124, 1994.
P. L. Bedard, M. K. Krzyzanowska, M. Pintilie, I. F. Tannock. Statistical Power of Negative Randomized Controlled Trials Presented at American Society for Clinical Oncology Annual Meetings. Journal of Clinical Oncology, 25:3482–3487, 2007.
C. G. Brown, G. D. Kelen, J. J. Ashton, H. A. Werman. The beta error and sample size determination in clinical trials in emergency medicine. Annals of Emergency Medicine, 16:183–187, 1987.
K. C. Chung, L. K. Kalliainen, R. A. Hayward. Type II (beta) errors in the hand literature: the importance of power. The Journal of Hand Surgery, 23:20–25, 1998. [↩] - 訳注:例えば実験動物を200匹使えば、十分な検定力が得られて、効果があると主張できるとしよう。この場合、誰かが最初に200匹を使って効果があると論文に書けば、犠牲になる実験動物は200匹しかいないことになる。しかし、実験する人がそろいもそろって50匹ずつしか使わなかった場合はどうなるだろうか。1人目は50匹しか使わず効果があると主張することに失敗する。2人目がまた別の50匹を使って効果があると主張することに失敗し、3人目がまた別の50匹を使って……ということが延々と続くことになる。50匹ずつ使った人が合わせて10人いたとすればその時点で500匹も実験動物が犠牲になる。誰かがこれら10人分のデータを集めて分析することがあれば、500匹分のデータがあるので効果があると主張できる。しかし、誰も集めなければ、500匹もの犠牲が生じた上に、何も知見が得られないということになってしまう。 [↩]
- 原注:K. S. Button, J. P. A. Ioannidis, C. Mokrysz, B. A. Nosek, J. Flint, E. S. J. Robinson, M. R. Munafò. Power failure: why small sample size undermines the reliability of neuroscience. Nature Reviews Neuroscience, 2013. [↩]
- 原注:E. Hauer. The harm done by tests of significance. Accident Analysis & Prevention, 36:495–500, 2004.
D. F. Preusser, W. A. Leaf, K. B. DeBartolo, R. D. Blomberg, M. M. Levy. The effect of right-turn-on-red on pedestrian and bicyclist accidents. Journal of Safety Research, 13:45–55, 1982. [↩]