文字列の類似度を測る(1) レーベンシュタイン距離

概要
ある文字列と別の文字列の類似度を測る手法の1つである、レーベンシュタイン距離について紹介する。文字列の類似度は検索エンジンやDNAの塩基配列の調査などにも使用されており、応用範囲は広い。

はじめに

Googleの検索結果の訂正候補
Googleの検索結果の訂正候補

検索サイトで検索語を間違えて入力してしまった場合、検索エンジンが訂正候補を出してくれることがある。図に掲げた例では、「マクドナルド」と入力しようとして、誤って「マクラナルド」と入力してしまっているが、Google は「マクドナルド」の検索結果を返している。誤ったものを入力すると、その誤ったものと似た正しいものを返しているのである。

このように訂正候補を出すには、まず入力されたものと似ているものを探し出すということが必要になる [1] 。そして、似ているものを探し出すには、何をもって似ているとするのかということを決めなくてはならない。つまり、類似度の尺度が必要となる。

今回は、ある文字列と別の文字列の類似度を測る手法の基礎について紹介してみたい。具体的には、最小編集距離、特にその中でもレーベンシュタイン距離というものについて見ていく。

文字列の類似度の応用範囲

冒頭で、文字列の類似度が用いられる例として、検索エンジンが訂正候補を出す例を挙げた。訂正候補を出すのは、検索エンジン以外にもあって、例えばワープロソフトのスペルチェッカーなどもその1つである。

訂正候補を出す場合以外にも文字列の類似度を使う場合はあり、例えば、DNAの塩基配列を調べるときにも使われる。DNAを構成する塩基はA, C, G, Tの4種類ある [2] 。この4種類の塩基をどう並べるかで、遺伝が決まってくる。要するに、DNAが表す遺伝情報とは、A, C, G, Tの4種類の文字で書かれる文字列なのである。DNAの塩基配列も文字列と見なせるから、類似度を測ることができるのである [3] 。

類似度と距離

以下では、文字列の類似度の尺度として、最小編集距離とかレーベンシュタイン距離といったものを見ていく。「類似度」について見ているのに、なぜ「距離」が出てくるのかといぶかしむ人もいるだろう。類似度と距離の関係について少し触れておこう。

類似度(similarity)と距離(distance)はほぼ同じ概念である。類似しているものは、距離が近いと考えられる。これに対して、類似していないものは距離が離れているというわけだ。基本的に言えば、類似の度合いは距離の遠近と同じことになる。

しかし、類似度と距離は完全に同じというわけではない。類似度の方がやや広い概念である。距離は、実は数学的にちゃんと定義された用語で、距離であるためには、距離の公理 [4] と呼ばれる条件を満たす必要がある。類似度と呼ばれるものの中には、距離の公理を満たさないものがたくさんあるので、距離でない類似度 [5] もあるということになる。

なお、もう1つ重要なこととして、距離にせよ類似度にせよ、その測定基準にはさまざまなものがあるということをおさえておいてもらいたい。例えば、自宅から最寄り駅までの距離を求める際に、長さに基づく直線距離で測ることもできるし、歩いたとしたら何分かかるかという時間的な距離で測ることもできる。

最小編集距離

文字列の類似度を測る際には、最小編集距離(minimum edit distance)というものがしばしば用いられる。これは、ある文字列にどれだけ編集を加えれば別の文字列になるか、ということに基づいて求められる距離である。編集の回数が多ければ多いほど、距離は大きくなる。例えば、「まくら」（枕）を「くらい」（位）にする場合、「まくら」から「ま」を外して「くら」にする編集と、「くら」に「い」をつけて「くらい」にする編集を行えばよい。つまり、「まくら」から「くらい」にするための編集は2回行う必要がある。よって、「まくら」から「くらい」までの最小編集距離は2になる。

なお、最小編集距離は、「最小」とついていることからも分かるように、最低限の編集回数で済むような編集の組み合わせを基準にして計算する。

実は、最小編集距離の中にも色々なものがある。それは、どういうものを編集として許すか、さらには編集の種類によって重み付けを変えるかどうかということと関わりがある。編集として何が許され、編集の種類の重み付けかがどうかということで、最小編集距離の定義が変わってきてしまうのである。

編集とは

文字列の編集方法としてさまざまなものがあるが、一般的には挿入・削除・置換の3種類だけを考える。最小編集距離の中でよく使われるレーベンシュタイン距離も挿入・削除・置換だけで考えている。

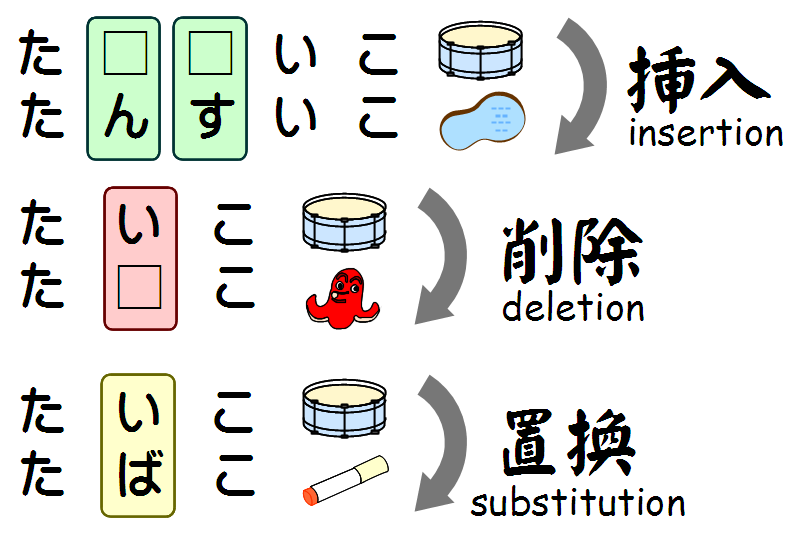
挿入・削除・置換という文字列の編集
挿入・削除・置換という文字列の編集

挿入(insertion)とは、ある文字列に文字を1つ入れることである。例えば、“can”（できる）の冒頭に“s”を挿入することで、“scan”（見渡す）になる。また、「あい」（藍）の間に「か」を挿入することで、「あかい」（赤い）になる。挿入の場合、あくまでも1回で1文字しか入れられない。「たいこ」（太鼓）を「たんすいこ」（淡水湖）にする場合、「すい」を一気に挿入することはできない。1回目の挿入で「す」、2回目の挿入で「い」と順を追って [6] 挿入しなくてはならない。

削除(deletion)とは、ある文字列から文字を1つ消すことである。例えば、“know”（知る）から“k”を削除することで、“now”（今）になる。また、「たいこ」（太鼓）から「い」を削除すれば、「たこ」（蛸）となる。

置換(substitution)とは、文字列の中の1文字を別の1文字に置き換えることである。例えば、“cat”（猫）の“a”を“u”に置換することで、“cut”（断つ）が得られる。また、「たいこ」（太鼓）の「い」を「ば」にすれば「たばこ」（煙草）が出てくる。

レーベンシュタイン距離

レーベンシュタイン距離(Levenshtein distance)は、最小編集距離の一種で、挿入・削除・置換が1回行われるごとに距離が1つ増えるような距離である。

具体例を見てみよう。「ちからうどん」（力うどん）と「からげんき」（空元気）の間のレーベンシュタイン距離を考えてみる。「ちからうどん」を「からげんき」にするためには、以下の4つの編集を行えば良い。

  1. 「ち」を削除する。
  2. 「う」を削除する。
  3. 「ど」を「げ」に置換する。
  4. 「き」を挿入する。
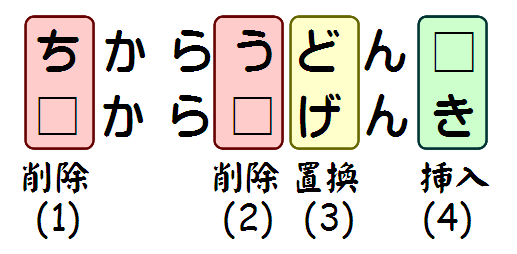
「ちからうどん」と「からげんき」のレーベンシュタイン距離
「ちからうどん」と「からげんき」のレーベンシュタイン距離

挿入にせよ、削除にせよ、置換にせよ、編集を1回行えばレーベンシュタイン距離は1だけ増える。この場合、編集は4回で済むから、「ちからうどん」（力うどん）と「からげんき」（空元気）の間のレーベンシュタイン距離は4になる。

計算機でレーベンシュタイン距離を求める

Google なら、ハトが単語の類似度を調べることも可能かもしれない [7] が、普通はハトは使わないで、計算機を用いてレーベンシュタイン距離を求めることになる。

レーベンシュタイン距離を求めるアルゴリズムについては、Wikipedia日本語版の「レーベンシュタイン距離」のページなどに書いてあるので、そちらを参照されたい。

Rでは、MiscPsycho パッケージに含まれる stringMatch コマンドでレーベンシュタイン距離を計算することができる。「ちからうどん」と「からげんき」のレーベンシュタイン距離を求めたい場合は、以下のようにコマンドを打ち込めば良い。

library(MiscPsycho)
stringMatch("ちからうどん", "からげんき", normalize="NO")

“normalize=”NO””を入れることに注意が必要である。入れない場合、距離が0から1の間の値を採るように標準化されてしまう。

なお、Rのデフォルトのコマンドで、“agrep”という曖昧検索をするコマンドがあるが、このコマンドでは、文字列の類似度を測るのに、レーベンシュタイン距離が用いられている。

脚注
  1. Google などの訂正候補の出し方はおそらくもっと複雑な仕組みで動いているはずだが。 [↩]
  2. A: アデニン、C: シトシン、G: グアニン、T: チミン。 [↩]
  3. 例えば、“CAATGG”は“CACTGG”とはよく似ているが、“AGTCCC”とは似ていないと言える。 [↩]
  4. 非負性（マイナスの距離は存在しない）・非退化性（同じもの同士の距離は0で、距離が0ならば同じもの同士の距離）・三角不等式（遠回りした方が距離は長くなる）・対称性（AからBまでの距離とBからAまでの距離は同じの4条件。詳しくは、Wikipedia日本語版の「距離空間」の項目を見ると良い。） [↩]
  5. 例えば、相関係数は類似度を示す尺度の1つだが、負の値をとる場合がある。距離は負の値にならないので、相関係数は距離ではない。 [↩]
  6. 1回目で「い」、2回目で「す」を挿入する順番でも構わない。要は1回の挿入で1文字ずつ入れることが重要なのである。 [↩]
  7. Googleテクノロジー PigeonRank™ を参照のこと。もちろんジョークですよ。 [↩]