はじめに
以前、文字列の類似度を測る手法として、レーベンシュタイン距離というものを紹介した。これは、ある文字列から別の文字列にする際に挿入・削除・置換を何回行うかに基づいて、文字列の類似度を測る尺度であった。レーベンシュタイン距離は簡便な指標であり、実際色々な分野で使われている。ただ、レーベンシュタイン距離だけでは捉えきれない問題もあって、そういう場合は、レーベンシュタイン距離以外の方法で文字列の類似度を測ることになる。
今回は、文字列の類似度を測るための尺度の中でも、レーベンシュタイン距離を拡張したものについて紹介していきたい。特に、Damerau–Levenshtein距離というものと、距離の標準化の話は重要になってくるので、おさえておくと何かと役に立つだろう。
編集方法
以前、レーベンシュタイン距離を紹介したときに、文字列の編集方法として挿入・削除・置換の3種類だけを考えると述べた。
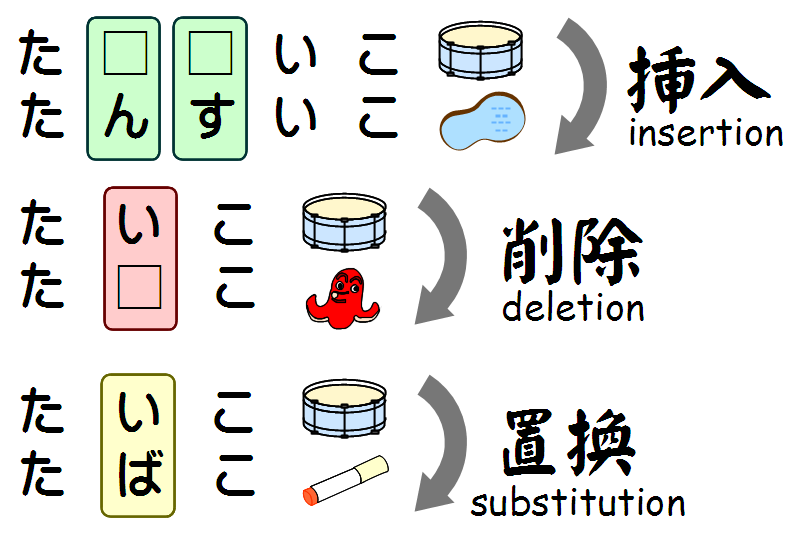
しかし、この3種類以外にも、編集方法として想定できるものがある。以下、転置という編集方法を中心に、移動・複写という編集方法について見ていこう [1] 。なお、移動・複写については考えないことが多いようなので、とりあえず転置だけ把握しておけば良いと思う。
転置
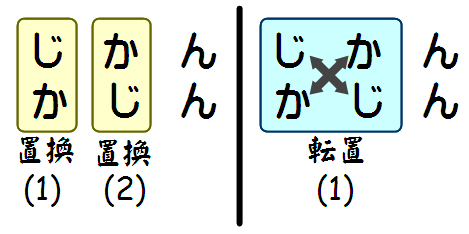
転置(transposition)とは、隣接する2つの文字の位置を入れ替えることである。例えば、「じかん」(時間)の「じ」と「か」を転置すると、「かじん」(歌人)になる。転置を編集方法として認めない場合、このような例では置換を2回行う必要がある。「じかん」から「かじん」にする場合は、先頭の「じ」を「か」にする置換と、真ん中の「か」を「じ」にする置換の合わせて2回の置換が必要になるのである。転置を認めれば、1回だけで済む。
転置はあくまでも隣接する文字同士で行う操作であって、隣接していない場合は普通は転置とは言わない [2] 。例えば「プール」と「ループ」では、「プ」と「ル」が入れ替わっているが、これは転置とは見なさない。
人間の言語の中で転置はしばしば起きる。例えば「雰囲気」という単語は、本来は「ふんいき」と発音するが、「ふいんき」と発音する人も少なくない。ここでは、「ん」と「い」の間で転置が起きているのである。また、サザンカという花があるが、これは漢字にすると「山茶花」であり、本来は「さんざか」と発音していた。「ん」と「ざ」の間で転置が起きた結果、「さんざか」が「さざんか」になったのである。なお、こういった人間の言語の中での転置のことを言語学的には音位転換(metathesis)と呼ぶ [3] 。
DNAの塩基配列でも、隣り合った位置にある塩基が入れ替わることはあるので、転置を含めて考えることは、DNAの分析にも役立つ [4] 。
移動
移動(move)は、1つの文字 [5] を別の位置に移すことである。例えば、「じかん」(時間)の先頭の「じ」を末尾に移動させることで、「かんじ」(漢字)が得られる。実は転置も移動の一種として捉えることができる。先ほど、「じかん」(時間)の「じ」と「か」を転置すると、「かじん」(歌人)になると述べた。これは「じかん」(時間)の「じ」を先頭の位置から「か」と「ん」の間の位置に移動させて「かじん」(歌人)となったと捉えることもできる。
上記の例では、1つの文字しか動かさなかった。ただ、これを拡張して、複数個の連続する文字を動かすということを考えた方が良いこともある。例えば、「やまあらし」(山嵐)の「やま」をまとめて末尾に移動すると、「あらしやま」(嵐山)が得られる類である。1回の編集で、複数個の連続する文字を動かすことを許すべきか否かは、調べたい現象によって変わってくる。もし、複数個の連続する文字が移動することがありふれたことであるならば、許した方が良いかもしれない。許すか許さないかについては絶対的な答えは無い。ただ、状況に応じて考えるしかない。
なお、挿入にせよ、削除にせよ、置換にせよ、基本的には1回の編集操作では文字1つ分しか手を加えない。複数個の文字を一気に編集するということはないのである。例えば、「たいこ」(太鼓)を「たんすいこ」(淡水湖)にするときは、1回の挿入で「すい」を入れると考えず、まず「す」を挿入してから「い」を挿入するという2回の編集であると考える。もちろん、移動の場合と同様に、複数個の連続する文字を対象にする挿入・削除・置換を考えても良い。ただ、挿入・削除・置換の場合、複数個の連続する文字を対象しても、文字列の類似度測定にあたってメリットがなさそうである。このため、挿入・削除・置換は1回の編集操作では文字1つ分に限って考える。
複写
複写(copy)は、文字列の一部分と同じものをもう1つ付け加えるような操作である。例えば、「かんご」(漢語)の「かん」を複写して、「かんごかん」(看護観)とするような例である。複写の対象は、1文字でも構わないし、複数個の連続する文字でも良い。この逆で、複写を解くような操作 [6] も考えることができる。「かんごかん」(看護観)で重複している「かん」を1つにして、「かんご」(漢語)や「ごかん」(互換)にするような例である。
Damerau–Levenshtein距離
レーベンシュタイン距離(Levenshtein distance)では、挿入・削除・置換の3種類しか編集方法として認めていなかった。Damerau–Levenshtein距離(Damerau–Levenshtein distance) [7] は、これに加え、転置も編集方法として認めている。つまり、Damerau–Levenshtein距離では、挿入・削除・置換・転置の4種類の編集方法が認められているわけである。
レーベンシュタイン距離の場合、「じかん」(時間)と「かじん」(歌人)の間の距離は2になる。これは、先頭の「じ」を「か」にする置換と、真ん中の「か」を「じ」にする置換の合わせて2回の編集を行うからである。これに対して、Damerau–Levenshtein距離では、転置を認めるので、「じ」と「か」の転置が1回起こったと考えれば良く、その距離は1になる。
移動・複写を編集方法として認める距離
レーベンシュタイン距離では編集方法として挿入・削除・置換の3種類を認め、Damerau–Levenshtein距離は挿入・削除・置換・転置の4種類を認めると先に述べた。移動や複写を認める距離も一応あるらしい [8] 。Graham Cormodeという人が、2003年にウォリック大学で出したSequence Distance Embeddings (PDF) という題名の博士論文の13ページには、Compression distanceという距離 [9] が挙げられている。このCompression distanceでは、編集方法として、挿入・削除・複写・uncopy [10] の4種類が認められている。また、同じ論文で、string edit distance with moves [11] という距離が挙げられている。これは、挿入・削除・移動 [12] の3種類の編集が認められている。
距離の標準化
レーベンシュタイン距離などは、今まで比較する文字列の長さというものは考えてこなかった。このため、直感的な文字列の類似度と一致しない場合が出てくる。例えば、「アイス」と「ノート」は同じ部分が全くなく、実感からすると全然類似していない。これに対して、「ミルクチョコレート」と「チョコレート」は、「ミルク」が付いているか付いていないかだけの違いであって、かなり類似しているという実感が持てるだろう。しかし、レーベンシュタイン距離を用いると、「アイス」と「ノート」の間の距離も、「ミルクチョコレート」と「チョコレート」の間の距離も、3になってしまう。レーベンシュタイン距離だけ見ると、両者の類似度は同じということになってしまう。
こういった実感との食い違いを防ぐために、標準化を行う必要が出てくる。標準化の方法はさまざまな手法が考えられるが、単純な手法としては、比較する文字列の長さで割るというものがある [13] 。この手法を採用すると、比較する文字列の長さに関係なく、距離が0以上1以下になるようにできる [14] 。比較する文字列の長さと言っても、2つの文字列の間で長さが異なる場合もある。こういった場合、長い方の文字列の長さで割るようにする。例えば、10文字の文字列と6文字の文字列を比べる場合、10で割ることで標準化すれば良い。
先ほどの例で言うと、「アイス」と「ノート」は素のレーベンシュタイン距離は3であった。これを文字列の長さの3で割って標準化すると、1になる。これに対し、「ミルクチョコレート」と「チョコレート」は素のレーベンシュタイン距離が3で、文字列の長さ9 [15] で割って標準化すれば、およそ0.33になる。このように標準化されたレーベンシュタイン距離(normalized Levenshtein distance)では、「アイス」と「ノート」は1とかけ離れており、「ミルクチョコレート」と「チョコレート」は0.33と近いという、実感に近い答えが出てくる。
なお、上記では、レーベンシュタイン距離について標準化の例を挙げたが、長さで割るという手法は他の距離にも応用できる。
Rでの標準化されたレーベンシュタイン距離の求め方
Rでは、MiscPsycho パッケージに含まれる stringMatch コマンドで標準化されたレーベンシュタイン距離を計算することができる。実は、stringMatch コマンドは何もデフォルトでは標準化されたレーベンシュタイン距離を出し、標準化されていないレーベンシュタイン距離を求めるためにはわざわざオプションを指定しなくてはいけない。「ちからうどん」と「からげんき」の標準化されたレーベンシュタイン距離を求めたい場合は、以下のようにコマンドを打ち込めば良い。
library(MiscPsycho)
stringMatch("ちからうどん", "からげんき")
なお、標準化されていないレーベンシュタイン距離を求める場合は、normalize=”NO”を指定する。
library(MiscPsycho)
stringMatch("ちからうどん", "からげんき", normalize="NO")
編集手法によって重み付けを変える
砂浜に何か単語を書いたとしよう。しばらく時間が経つと、字が消えたり(削除)、他の字のように見えたり(置換)するようなことが起こるだろう。しかし、字が加わる(挿入)ということは、あまり起きそうにはない。つまり、この場合、削除や置換にはさほどコストがかからないのに対し、挿入にはコストがかなり必要になっている。
今までは、距離を求める場合、どの編集も1回行えば、距離が1だけ増えると考えていた。しかし、どの編集でも同じコストであると考えなくてはならない必然性はどこにもない。編集方法によって、重み付けを変えるということがあっても良いのである。例えば、削除は重みが1だが、挿入は3にするとかいうことがありうる。このようにして、重み付けがある編集距離(weighted edit distance)を考えることができるのである。
- なお、以下の編集方法に関する記述は、以下の書籍の201-202ページの内容を参考にした。Deza, M. M. & Deza, E. (2009). Encyclopedia of Distances. Berlin: Springer. [↩]
- 隣接するもの同士の方が入れ替えが起こりやすいから、隣接するものを重視することには合理的な理由がある。タイプの例を考えると、“racket”(ラケット)を“racekt”とミスしてしまうように、隣接するものが入れ替わることが、しばしば見られる。 [↩]
- 転置は隣接しているものだけに限ると言ったが、音位転換の場合、実は隣接していなくても良い。 [↩]
- 前に触れたように、DNAの塩基配列は、A, T, C, Gの4つの文字を使う文字列と考えることができるので、文字列の類似度を測る手法で研究することができる。 [↩]
- 直後で見るように、1つの文字に限らず、複数の連続する文字を動かす場合も1回の移動と考えることがある。 [↩]
- 英語で言えば、uncopy。良い和訳は思いつかない。 [↩]
- Levenshteinのことをそのまま仮名でレーベンシュタインとする例はよく見るが、Damerauを仮名にしている例は見たことがない。そもそも、私は、Damerauの発音がよく分からないので、だれか知っている人がいたら教えてください。 [↩]
- 「あるらしい」と書いたのは私がよく分かっていないため。このような距離をどういう用途で使うのかもよく分からない。 [↩]
- 和訳すると、「圧縮距離」となるだろうか。正規化圧縮距離(normalized compression distance; NCD)とは別物。 [↩]
- uncopyとは、複写を解くような操作のこと。 [↩]
- 和訳すれば、「移動を含む文字列編集距離」。 [↩]
- 挿入と削除は1文字単位でしか行えないが、移動は複数個の連続する文字を一気に動かすことが可能。 [↩]
- 今考えている距離は、重み付けの無い距離であって、この場合単純に文字列の長さで割れば良い。しかし、重み付けのある距離の場合、そう単純にはいかなくなる。重み付けのある距離における標準化の手法は以下の文献を参照のこと。Marzal, A. & Vidal, E. (1993). Computation of Normalized Edit Distance and Applications. IEEE Transactions on Pattern Analysis and Machine Intelligence 15, 926-932. [↩]
- 比較する文字列同士が完全に一致するならば距離は0、まったく一致する場所が無いようならば距離は1になる。 [↩]
- 「ミルクチョコレート」と「チョコレート」では長さが異なるが、そういった場合は、長い方で割るのであった。 [↩]