【翻訳】整然データ

概要
効果的なデータ分析に関して、「整然データ」という概念を提唱した論文 “Tidy Data” の全訳。整然データは、Rなどでデータ分析を容易にする有用な概念である。

訳者前書き

ここに公開するのは、以下の論文の全訳である。

この論文は、「整然データ」(tidy data) という概念を提唱したものである。これは、Rなどでデータ分析を容易にする有用な概念になっている。

なお、この概念についての簡単な解説として、「整然データとは何か」という文章を用意したので、先をそちらを読んでもよいだろう。また、“tidy” という英語をなぜ「整然」という日本語に訳したかについては「なぜ“tidy data”を「整然データ」と訳したのか」という記事を参照のこと。

なお、本サイトに公開する前に、翻訳に関して githubを通じて松原勇介 (whym) 氏と神谷年洋 (tos-kamiya) 氏から貴重なコメントをいただいた。ここで改めて感謝したい。

要約

分析準備のためのデータクリーニングに対して膨大な労力が費やされているが、できるだけ簡単で効果的にデータクリーニングを行う手法についてはほとんど研究がなされていない。 本論文では、データクリーニングにおいて、小さなことではあるが重要な要素であるデータの整然化に取り組む。整然データセットは、操作・モデル化・視覚化が容易であり、特有の構造を持っている。すなわち、個々の変数が列となり、個々の観測が行となり、個々の観測の構成単位の類型が表となる。 このフレームワークは、幅広い範囲の非整然データセットに対処するためにわずかな数のツールしか必要としないことから、雑然データセットを整然化することを容易にする。 この構造は、データ分析のために、整然ツール、すなわち入力と出力がいずれも整然データセットとなるツールを開発することをも容易にする。 一貫したデータ構造とそれに合ったツールの利点は、面白みのないデータ操作の雑用から解放された事例研究で実証される。

はじめに

データ分析の80%がデータのクリーニングと準備の過程に費やされていると言われることがしばしばある (Dasu & Johnson 2003)。データの準備は、最初の段階だけにかぎられものではない。新しい問題が発生したり、新しいデータが収集されたりするたびに、分析の過程で何度も繰り返し行われる必要があるのだ。しかし、その費やされる時間の総量が膨大なものであるにもかかわらず、データをうまくクリーニングする方法についての研究は、驚くほど少ない。その難しさの一面として、含まれる作業の範囲の広さがある。作業の範囲としては、外れ値の確認から、日付の解析、欠損値の追究まである。本論文では、この問題に対処するために、データクリーニングにおける小さなことであるが重要な側面に着目する。データの整然化 (tidying) と呼ぶことになるこの側面は、分析を容易にするために、データセットを構造化することを指す。

整然データの原理により、データセットの内部のデータ値を編成するための標準的手法が提供される。標準があることで、毎回何もないところから始めたり、車輪の再発明をしたりする必要がなくなるため、最初のデータクリーニングが容易になる。整然データの標準は、データに対する最初の探索と分析を容易にし、効率的に連携するデータ分析ツールの開発を簡単にするように設計されている。現行のツールは、しばしば翻訳が必要となる。別のツールに入力できるようにするには、あるツールからの出力を大規模に変更するための時間を費やす必要がある。整然データセットと整然ツールは、データ分析をより簡単にするために、協同して働く。このことにより、データに関する興味のない兵站処理でなく、興味のある領域の問題に集中することができる。

整然データの原理は、リレーショナルデータベースの原理やコッドのリレーショナル代数 (Codd 1990) の原理と密接に関連している。ただし、整然データの原理は、統計分析者が慣れた言葉で表現されている。計算機科学者も、データクリーニングの研究に大いに貢献してきた。例えば、Lakshmanan, Sadri & Subramanian (1996) は、雑然データセットを操作できるようにSQLの拡張を定義した。また、Raman and Hellerstein (2001) はデータセットをクリーニングするための枠組みを提供した。Kandel, Paepcke & Hellerstein (2011) は、データクリーニングのためのコードを自動的に生成する親しみやすいユーザーインターフェイスを備えた対話型ツールを開発している。これらのツールは有用であるが、ほとんどの統計分析者にとってなじみのない言語で書かれており、データセットをどのように構造化すべきかについての助言をさして提供することができておらず、データ分析ツールとのつながりを欠いている。

整然データは、実世界のデータセットに取り組んだ私の経験を通じて発展してきた。実世界のデータセットはしばしば奇怪な方法で構築される。編成に関する制約があったとしてもほんのわずかしかないないためである。そのようなデータセットをデータ分析が可能になるような整ったものにすることに、私は非常に長い時間を費やしてきた。そして、データ分析が容易になるようにもしてきた。さらに、学生が自ら実世界のデータセットに対処できるように、こうしたスキルを学生に伝えることにも取り組んできた。こうした取り組みの過程で、私は reshape と reshape2 (Wickham 2007) というパッケージを開発した。私は直感的にこれらのツールを使い、事例を通じて学生に教えることができたが、私の直感を明示的なものにするための枠組みはなかった。本論文はそのための枠組みを提供する。この枠組みは、包括的な「データの哲学」(philosophy of data) を提供する。これは、私のたずさわった plyr (Wickham 2011) と ggplot2 (Wickham 2009) パッケージの根底にあるものである。

本論文は以下のように議論を進める。第2節では、データセットを整然たらしめる3つの特性を定義することから始める。実世界のデータセットのほとんどが整然でないことを踏まえ、第3節では、雑然データセットを整然たらしめるために必要な操作について記述し、さまざまな実例を使って技法を説明する。第4節では、整然データセットを入出力するツールである整然ツールを定義し、どのように整然データと整然ツールが協同してデータ分析を容易にするかについて議論する。これらの原理は、第5節で扱う小規模な事例研究で説明される。最後に、第6節では、結論として、この枠組みが見逃していることについて論じ、さらに他のどのようなアプローチがさらなる追究に有益である可能性があるかについて論じる。

整然データの定義

幸福な家族はどれも似ているが、不幸な家族は不幸のあり方がそれぞれ異なっている。

レフ・トルストイ

家族と同じく、整然データセットはどれも似ているが、雑然データセットは雑然のあり方がそれぞれ異なっている。整然データセットは、データセットの構造（物理レイアウト）をその意味と結びつけるための標準的手法を提供する。この節では、データセットの構造と意味を記述するための基準となる用語をいくつか準備した上で、そうした用語の定義をもって整然データを定義する。

データ構造

ほとんどの統計データセットは、行 (row) と列 (column) からなる長方形の表となっている。ほとんどすべての場合、列にはラベルが付される。行には、時々ラベルが付される。表1は、架空の実験に関するデータを、野生の状態で一般的に見られる形式で示したものである。この表には、2つの列と3つの行があり、行と列の両方にラベルが付されている。

表1：典型的な発表用データセット。
treatmenta treatmentb
John Smith ― 2
Jane Doe 16 11
Mary Johnson 3 1

同じ潜在的データに対して、それを構造化する方法は数多く存在する。表2は、表1と同じデータを示すが、行と列とが転置されている。データは同じであるが、レイアウトが異なっている。行や列といった用語は、2つの表が同じデータを表す理由を記述するのにとても十分なものではない。外観に加えて、表に示された値の潜在的意味を記述する方法が必要になる。

表2：表1と同じデータだが、構造化の方法が異なっている。
John Smith Jane Doe Mary Johnson
treatmenta ― 16 3
treatmentb 2 11 1

データの意味

データセットとは値 (value) を集めたものである。値は、通常、数（量的なものの場合）か文字列（質的なものの場合）のいずれかになる。値は、2つの方法でまとめられる。どの値も、1つの変数 (variable) に属し、なおかつ1つの観測 (observation) に属する。変数には、さまざまな構成単位に対して、同じ潜在属性（高さ、温度、継続時間など）を測定するすべての値が含まれる。観測には、さまざまな属性に対して、同じ構成単位（1人、1日、1レースなど）で測定されたすべての値が含まれる。

表3は、値・変数・観測をより明確にするために、表1を再編成したものである。データセットには、3つの変数と6つの観測を表す18個の値が含まれている。ここで、変数には以下のものがある。

  1. person（人）：取りうる値を3つ (John Smith, Mary Johnson, Jane Doe) 持つ。
  2. treatment（処置）：取りうる値を2つ (a, b) 持つ。
  3. result（結果）：欠損値をどう捉えるかによって変わるが、取りうる値を5つまたは6つ (―, 16, 3, 2, 11, 1) 持つ。

実験計画から、観測の構造についてより詳しいことが分かる。この実験は、完全に交差した計画であり、person（人）とtreatment（処置）のすべての組み合わせが測定された。また、実験計画は、欠損値を安全に捨て去ることができるかどうかについても決定する。この実験では、欠損値は、なされるべきだったがなされなかった観測を表しているので、それを保持しておくことは重要である。なすことができない測定（例：妊娠したオスの数）を表す構造的欠損値は、安全に捨て去ることができる。

表3：表1と同じデータだが、変数が列に、観測が行になっている。
name treatment result
John Smith a —
Jane Doe a 16
Mary Johnson a 3
John Smith b 2
Jane Doe b 11
Mary Johnson b 1

通常、所与のデータセットに対して何が変数で何が観測かを把握するのは容易である。しかし、変数や観測について、一般的な定義を正確に行うことは驚くほど困難である。例えば、表1の列がheight（高さ）と weight（重量）であったとしたら、それらを変数と呼ぶことは納得がいくだろう。列が height（高さ）とwidth（幅）であったとしたら、高さと幅をdimension（次元）変数の値と考える可能性があるので、あまり明確ではなくなるだろう。列がhome phone（自宅の電話）とwork phone（職場の電話）であったとしたら、これらを2つの変数として扱うことができるものの、不正検知の環境では、複数の人が1つの電話番号を使用していることが不正を示唆する可能性があるため、phone number（電話番号）とnumber type（電話番号の種別）という変数が欲しくなるかもしれない。一般的な経験則としては、行と行の間よりも、変数と変数の間の関数的関係を記述する方が容易である（例：zはxとyの線形結合である、density（密度）はweight（重量）とvolume（体積）の比である）。また、行のグループと行のグループとの間よりは、観測のグループと観測のグループの間の比較の方が容易である（例：グループaの平均とグループbの平均の比較）。

所与の分析に対して、複数のレベルの観測が存在しうる。例えば、新しいアレルギー薬の試験では、観測に3種類のものがあるだろう。すなわち、人ごとに収集される人口統計学上のデータ（age「年齢」・sex「性別」・race「人種」）、日ごとにかつ人ごとに収集される医療上のデータ（number of sneezes「くしゃみの数」・redness of eyes「目の赤み」）、日ごとに収集される気象データ（temperature「温度」・pollen count「花粉数」）である。

整然データ

整然データは、データセットの意味をその構造に写し取る標準的手法である。 データセットが雑然か整然かは、行・列・表が、観測・変数・類型とどれだけ一致しているかによって決まる。整然データ (tidy data) には以下の性質がある。

  1. 個々の変数が1つの列をなす。
  2. 個々の観測が1つの行をなす。
  3. 個々の観測の構成単位の類型が1つの表をなす。

これは Codd の第3正規形 (Codd 1990) であるが、統計の言語に合わせた制約がある。そして、リレーショナルデータベースでよく使われるような多くの接続されたデータセットではなく、単一のデータセットに重点が置かれている。雑然データ (messy data) は、整然データ以外のデータの配列方法を指す。

表3は、表1の整然化されたバージョンである。個々の行は、1人のperson（人）に対する1回のtreatment（処置）のresult（結果）である観測1回分を表す。そして、個々の列は変数1つを表す。

整然データは、データセットを構造化する標準的手法を提供するため、分析者や計算機が必要な変数を抽出することを容易にする。表3を表1と比較してみよう。表1では、異なる変数を抽出するのに、異なる戦略を使用する必要がある。これにより、分析が遅くなり、エラーがもたらされる。ある変数に属するすべての値に関わるデータ分析操作（すべての集計関数）の数を考慮すれば、単純かつ標準的手法でこれらの値を抽出することが重要であることが分かるだろう。 整然データは、R (R Core Team 2014) のようなベクトル化されているプログラミング言語に特に適している。なぜかと言えば、そのレイアウトによって、同じ観測からの異なる変数の値が常にペアになることが保証されているためである。

変数と観測の順序は分析に影響しないが、順序を適切にすれば、生の値を読み取ることが容易になる。変数を編成する方法の1つとして、分析における変数の役割によって考えるというものがある。つまり、データ収集計画によって固定された値であるか、それとも、実験の過程で測定される値であるかと考えるのだ。固定変数は、実験計画を記述したもので、事前に分かっているものである。計算機科学者はしばしばそれらを固定変数の次元と呼び、統計学者は通常それらを確率変数の添字で示す。被測定変数は、我々が研究で実際に測定するものである。固定変数が最初に来るべきで、被測定変数がそれに続くようにすべきである。そして、関連する変数が連続するように各々の変数を並べるべきである。そして、行は最初の変数によって並べられ、2番目以降の（固定）変数との結びつきはなくなる。これは、本論文で表の形で示したものがすべて従っている方式である。

雑然データセットの整然化

実際のデータセットは、想像のつくほとんどすべての方法で整然データの3つの指針に違反しうる。そして、違反することは実際にしばしばある。時には即座に分析を開始できるデータセットが得られることもあるが、これは例外であって、いつもそうなるわけではない。本節では、雑然データセットに関する以下の5つの最も一般的な問題について説明する。あわせて、これらの問題への対処方法も説明する。

ほとんどの雑然データセットは、上で明示的に触れられていないたぐいの雑然さを含んでいるのだが、驚くべきことに、融解・文字列分割・鋳造といった少数のツールを使えば整然化可能である。本節では、私が遭遇したことのある実際のデータセットに基づいて、各々の問題について説明し、それらを整然化する手法を示す。完全なデータセットとそれを整然化するために使用したRのコードは、https://github.com/hadley/tidy-data からオンラインで入手できる。また、本論文のオンラインの補充資料からも入手できる。

列見出しが、値であって変数名でない

ありふれたたぐいの乱雑データセットとして、プレゼンテーション用にデザインされたある種の表の形をしたデータがある。こうしたデータセットでは、変数が行にも列にもなり、列見出しは変数名 (variable name) でなく値になっている。私はこうした配列方法を雑然なものと見なしているが、場合によってはこれが非常に便利なこともある。この種のデータセットは、完全に交差した設計においては、記憶容量の面で効率的になる。さらに、希望する操作が行列演算として表現できる場合、計算が非常に効率的になる。このことについては、第6節で詳しく議論する。

表4は、この形式の典型的なデータセットの一部を示したものである。このデータセットは、米国における所得と宗教との関係を調査したもので、米国のシンクタンクであるピュー・リサーチ・センター (Pew Research Center) が作成したレポート [1] から持ってきたものだ。ピュー・リサーチ・センターは、宗教からインターネットまでの幅広い主題に対する態度についてのデータを収集し、この形式のデータセットを載せた数多くのレポートを作成している。

表4：ピュー・フォーラムから取った収入と宗教に関するデータの最初の10行。3列 ($75-100k, $100-150k, >150k) が省略されている。
religion <$10k $10-20k $20-30k $30-40k $40-50k $50-75k
Agnostic 27 34 60 81 76 137
Atheist 12 27 37 52 35 70
Buddhist 27 21 30 34 33 58
Catholic 418 617 732 670 638 1116
Don’t know/refused 15 14 15 11 10 35
Evangelical Prot 575 869 1064 982 881 1486
Hindu 1 9 7 9 11 34
Historically Black Prot 228 244 236 238 197 223
Jehovah’s Witness 20 27 24 24 21 30
Jewish 19 19 25 25 30 95

このデータセットには、religion（宗教）、income（収入）、frequency（頻度）という3つの変数がある。これを整然化するには、融解 (melt) する必要がある（融解の代わりに「スタック」 [stack] とも言う）。つまり、列を行に変換する必要があるのだ。これは、幅広 (wide) のデータセットを長い (long/tall) ものにすると表現されることがしばしばある。しかし、こう表現するのは不正確であるから、この言い方は避けたいと思う。融解は、既に変数 (variable) となっている列 (column) のリスト（略してcolvarと呼ぶ）がパラメータとなっている。まだ変数となっていない他の列は、2つの変数に変換される。すなわち、列見出しの繰り返しを含むcolumn（列）という新しい変数と、前は分かれていた列から持ってきた値をつなぎ合わせたものを含むvalue（値）という新しい変数である。このことは、ごく小さなデータセットを用いて表5に示されている。融解の結果は融解されたデータセット (molten dataset) である。

表5(a)：融解の簡単な例。(a) は row（行）という1個のcolvarにより融解され、融解されたデータセットである (b) が得られる。どちらの表もまったく同じ情報を表している。異なるのは、格納方法だけである。
row a b c
A 1 4 7
B 2 5 8
C 3 6 9
表5(b)：融解の簡単な例。(a) は row（行）という1個のcolvarにより融解され、融解されたデータセットである (b) が得られる。どちらの表もまったく同じ情報を表している。異なるのは、格納方法だけである。
row column value
A a 1
B a 2
C a 3
A b 4
B b 5
C b 6
A c 7
B c 8
C c 9

ピューのデータセットには、colvarが1つある。それはreligion（宗教）である。そして、融解することで表6が得られる。このデータセットでの役割をよりうまく反映するために、variable（変数）の列はincome（収入）に、value（値）の列はfreq（頻度）に名前を変更してある。この形式は、整然である。なぜかと言えば、個々の列が変数を表し、個々の行が観測を表し、さらに、この場合は人口統計学上の個々の構成単位がreligion（宗教）とincome（収入）の組み合わせに対応しているからだ。

表6：整然化されたピューの収入と宗教に関する調査のデータセットの最初の10行。column（列）の列はincome（収入）に、value（値）の列はfreq（頻度）に名前を変更してある。
religion income freq
Agnostic <$10k 27
Agnostic $10-20k 34
Agnostic $20-30k 60
Agnostic $30-40k 81
Agnostic $40-50k 76
Agnostic $50-75k 137
Agnostic $75-100k 122
Agnostic $100-150k 109
Agnostic >150k 84
Agnostic Don’t know/refused 96

このデータフォーマットのもう1つの一般的な使用方法として、時間の経過とともに定期的に観測を記録するものが挙げられる。例えば、表7に示すビルボード (Billboard) データセットには、曲が最初にビルボード・トップ100 (Billboard Top 100) に入った日付が記録されている。ここには、artist（アーティスト）、track（トラック）、date.entered（入った日付）、rank（順位）、week（週）という変数がある。トップ100に入った後の各週のランクは、wk1からwk75までの75個の列に記録される。曲がトップ100に入っている期間が75週に満たない場合、残りの列は欠損値で埋められる。この格納形式は整然ではないが、データ入力には便利である。そうしなければ、毎週曲ごとに独自の行が必要となり、タイトルやアーティストといった曲のメタデータを繰り返さす必要が出てきてしまう。しかし、この格納形式を用いれば、繰り返しが少なくなる。この問題については、3.4節でさらに詳しく説明する。

表7：2000年のビルボード・トップヒットの最初の8個。他の示されていない列として、wk4, wk5, …, wk75がある。
year artist track time date.entered wk1 wk2 wk3
2000 2 Pac Baby Don’t Cry 4:22 2000-02-26 87 82 72
2000 2Ge+her The Hardest Part Of … 3:15 2000-09-02 91 87 92
2000 3 Doors Down Kryptonite 3:53 2000-04-08 81 70 68
2000 98^0 Give Me Just One Nig… 3:24 2000-08-19 51 39 34
2000 A*Teens Dancing Queen 3:44 2000-07-08 97 97 96
2000 Aaliyah I Don’t Wanna 4:15 2000-01-29 84 62 51
2000 Aaliyah Try Again 4:03 2000-03-18 59 53 38
2000 Adams, Yolanda Open My Heart 5:30 2000-08-26 76 76 74

このデータセットには、year（年）、artist（アーティスト）、track（トラック）、time（時間）、date.entered（入った日付）という colvar がある。これを融解すると表8が得られる。ここで整然化だけでなく、クリーニングを少々実施した。すなわち、column（列）は数を取り出すことでweek（週）に変換した。また、date（日付）をdate.entered（入った日付）とweek（週）から計算した。

表8：整然化されたビルボードデータセットの最初の15行。date（日付）の列は、元の表には出てこないが、date.entered（入った日付）とweek（週）から計算できる。
year artist time track date week rank
2000 2 Pac 4:22 Baby Don’t Cry 2000-02-26 1 87
2000 2 Pac 4:22 Baby Don’t Cry 2000-03-04 2 82
2000 2 Pac 4:22 Baby Don’t Cry 2000-03-11 3 72
2000 2 Pac 4:22 Baby Don’t Cry 2000-03-18 4 77
2000 2 Pac 4:22 Baby Don’t Cry 2000-03-25 5 87
2000 2 Pac 4:22 Baby Don’t Cry 2000-04-01 6 94
2000 2 Pac 4:22 Baby Don’t Cry 2000-04-08 7 99
2000 2Ge+her 3:15 The Hardest Part Of … 2000-09-02 1 91
2000 2Ge+her 3:15 The Hardest Part Of … 2000-09-09 2 87
2000 2Ge+her 3:15 The Hardest Part Of … 2000-09-16 3 92
2000 3 Doors Down 3:53 Kryptonite 2000-04-08 1 81
2000 3 Doors Down 3:53 Kryptonite 2000-04-15 2 70
2000 3 Doors Down 3:53 Kryptonite 2000-04-22 3 68
2000 3 Doors Down 3:53 Kryptonite 2000-04-29 4 67
2000 3 Doors Down 3:53 Kryptonite 2000-05-06 5 66

複数の変数が、1つの列に格納されている

融解後、column（列）変数の名前は、多くの場合、複数の潜在的変数の名称を組み合わせたものになる。このことは、結核 (TB) データセットによって示されており、その標本が表9に表されている。このデータセットは、世界保健機関からのものであり、確認された結核の症例数をcountry（国）、year（年）、そして、人口統計学上のグループ別に記録している。人口統計学上のグループはsex（性別〔男、女〕）とage（年齢〔0-14, 15-25, 25-34, 35-44, 45-54, 55-64, 不明〕）によって分類されている。

表 9：元のTBデータセット。男を示す‘m’列のそれぞれに対応して、f1524, f2534といった女性を示す‘f’列もある。紙幅の関係でこれらの列は示されていない。0と欠損値（—）が混ざっていることに気をつけよう。これはデータ収集の過程に起因するもので、このデータセットにおいては両者を区別することが重要になる。
country year m014 m1524 m2534 m3544 m4554 m5564 m65 mu f014
AD 2000 0 0 1 0 0 0 0 — —
AE 2000 2 4 4 6 5 12 10 — 3
AF 2000 52 228 183 149 129 94 80 — 93
AG 2000 0 0 0 0 0 0 1 — 1
AL 2000 2 19 21 14 24 19 16 — 3
AM 2000 2 152 130 131 63 26 21 — 1
AN 2000 0 0 1 2 0 0 0 — 0
AO 2000 186 999 1003 912 482 312 194 — 247
AR 2000 97 278 594 402 419 368 330 — 121
AS 2000 — — — — 1 1 — — —

この形式の列見出しは、多くの場合、何らかの文字 (., -, _, :)で区切られいる。こうした場合は、これらの文字を分割のために用いて、文字列を要素に分けることが可能がである。しかし、このデータセットのようにそうではない場合は、より入念な文字列処理が必要となる。例えば、単一の複合値を複数の構成要素の値に変換するルックアップテーブルを用い、変数名をマッチさせることができる。

表10(a) はTBデータセットを融解した結果を示し、表10(b) はcolumn（列）という1個の列をage（年齢）とsex（性別）という2つの実際の変数に分割した結果を示している。

表10(a)：TBデータセットを整然にするには、最初に融解を実施した上で、column（列）という列をage（年齢）とsex（性別）の2つの変数に分ける必要がある。
country year column cases
AD 2000 m014 0
AD 2000 m1524 0
AD 2000 m2534 1
AD 2000 m3544 0
AD 2000 m4554 0
AD 2000 m5564 0
AD 2000 m65 0
AE 2000 m014 2
AE 2000 m1524 4
AE 2000 m2534 4
AE 2000 m3544 6
AE 2000 m4554 5
AE 2000 m5564 12
AE 2000 m65 10
AE 2000 f014 3
表10(b)：TBデータセットを整然にするには、最初に融解を実施した上で、column（列）という列をage（年齢）とsex（性別）の2つの変数に分ける必要がある。
country year sex age cases
AD 2000 m 0-14 0
AD 2000 m 15-24 0
AD 2000 m 25-34 1
AD 2000 m 35-44 0
AD 2000 m 45-54 0
AD 2000 m 55-64 0
AD 2000 m 65+ 0
AE 2000 m 0-14 2
AE 2000 m 15-24 4
AE 2000 m 25-34 4
AE 2000 m 35-44 6
AE 2000 m 45-54 5
AE 2000 m 55-64 12
AE 2000 m 65+ 10
AE 2000 f 0-14 3

この形式で値を格納すると、元のデータの別の問題が解決される。我々は、数でなく、率を比較したいのだ。しかし、率を計算するには、人口を知る必要がある。元の形式では、人口という変数を追加するための簡単な手法はない。別の表に格納する必要があるため、人口と数を正確にマッチさせることは困難である。整然形式では、人口と率の変数を追加するのは容易である。単に列を追加するだけである。

変数が、行と列の両方に格納されている

雑然データの最も複雑な形式は、変数が行と列の両方に格納されているものである。表11は、世界歴史気候学ネットワーク (Global Historical Climatology Network) からのデータで、メキシコのある気象観測所 (MX17004) における2010年の5か月にわたる毎日の気象データを示している。変数としては、単独の列（id、year〔年〕、month〔月〕）、複数列にわたっているもの（day〔日〕、d1-d31）、複数行にわたっているもの（tmin〔最低気温〕、tmax〔最高気温〕）といった形のものがある。31日に満たない月は、その月の最後の方の日が構造的な欠損値になる。element（要素）列は変数ではなく、変数名を格納している。

このデータセットを整然化するには、まず colvar であるid、year〔年〕、month〔月〕と変数名を含む列であるelement（要素）を使って融解する。これにより表12(a) が得られる。体裁のために、欠損値を落とし、欠損値を明示的でなく暗黙的に表した。月ごとの日数が分かっていて、明示的欠損値を簡単に再構築できるため、このことは許容される。

このデータセットはほぼ整然化されているが、行に格納されているtmin（最低気温）とtmax（最高気温）という2種類の変数がある。この例では、他の気象に関する変数である prcp（降水量）とsnow（降雪量）は表示されていない。観測の種類に関する問題を解決するには、鋳造操作（鋳造 [cast] の代わりに「アンスタック」 [unstack] とも言う）が必要となる。この操作では、element（要素）変数を回転して列に戻すことで融解の逆の操作を実行する（表12(b)）。この表の形式は整然である。各列には1つの変数があり、各行は1日の観測を示している。鋳造操作については、Wickham (2007) で詳細に説明されている。

表11：元の天候のデータセット。月の中で可能な日のすべてについて個別の列がある。d9列からd31列は紙幅の関係で省略されている。
id year month element d1 d2 d3 d4 d5 d6 d7 d8
MX17004 2010 1 tmax — — — — — — — —
MX17004 2010 1 tmin — — — — — — — —
MX17004 2010 2 tmax — 27.3 24.1 — — — — —
MX17004 2010 2 tmin — 14.4 14.4 — — — — —
MX17004 2010 3 tmax — — — — 32.1 — — —
MX17004 2010 3 tmin — — — — 14.2 — — —
MX17004 2010 4 tmax — — — — — — — —
MX17004 2010 4 tmin — — — — — — — —
MX17004 2010 5 tmax — — — — — — — —
MX17004 2010 5 tmin — — — — — — — —
表12(a)：融解された天候のデータセット。これはほとんど整然であるが、element（要素）列が、値ではなく変数の名前を含んでいる。欠損値は紙幅の関係で削ってある。
id date element value
MX17004 2010-01-30 tmax 27.8
MX17004 2010-01-30 tmin 14.5
MX17004 2010-02-02 tmax 27.3
MX17004 2010-02-02 tmin 14.4
MX17004 2010-02-03 tmax 24.1
MX17004 2010-02-03 tmin 14.4
MX17004 2010-02-11 tmax 29.7
MX17004 2010-02-11 tmin 13.4
MX17004 2010-02-23 tmax 29.9
MX17004 2010-02-23 tmin 10.7
表12(b)：整然な天候データセット。各行が単一の日付における気象測定を示している。tmin（最低気温）とtmax（最高気温）という2つの測定された変数がある。それ以外の変数は固定的なものである。
id date tmax tmin
MX17004 2010-01-30 27.8 14.5
MX17004 2010-02-02 27.3 14.4
MX17004 2010-02-03 24.1 14.4
MX17004 2010-02-11 29.7 13.4
MX17004 2010-02-23 29.9 10.7
MX17004 2010-03-05 32.1 14.2
MX17004 2010-03-10 34.5 16.8
MX17004 2010-03-16 31.1 17.6
MX17004 2010-04-27 36.3 16.7
MX17004 2010-05-27 33.2 18.2

1つの表に複数の類型がある

データセットには、観測の構成単位のさまざまな類型について、複数のレベルで収集された値が含まれることがある。整然化の間は、観測の構成単位の各類型は、それ独自の表に格納されるべきである。これは、個々の事実が1つの場所においてのみ表現されるというデータベースの正規化の考え方と密接に関連している。これが行われないと、不一致が発生する可能性がある。

表8に示されているビルボードデータセットには、実際のところ、観測の構成単位の類型が2つ（曲、その各週の順位）含まれている。このことは、曲に関する事実が重複していることに表れている。つまり、artist（アーティスト）とtime（時間）が、個々の週において、曲ごとに繰り返されているのだ。ビルボードデータセットは、2つのデータセットに分ける必要がある。すなわち、artist（アーティスト）、song name（曲名）、time（時間）を格納する曲データセット、およびweek（週）ごとのsong（曲）のrank（順位）を示す順位データセットである。表13は、これら2つのデータセットを示している。週ごとに、その週に売れた曲の総数や類似の人口統計学的情報といった週に関する背景情報を記録しているような、週のデータセットを想定することもできるだろう。

表13：曲データセット（上）と順位データセット（下）に分けられ、正規化されたビルボードデータセット。各々のデータセットの最初の15行が示されている。曲データセットからはgenre（ジャンル）が、順位データセットからはweek（週）が割愛されている。
id artist track time
1 2 Pac Baby Don’t Cry 4:22
2 2Ge+her The Hardest Part Of … 3:15
3 3 Doors Down Kryptonite 3:53
4 3 Doors Down Loser 4:24
5 504 Boyz Wobble Wobble 3:35
6 98^0 Give Me Just One Nig… 3:24
7 A*Teens Dancing Queen 3:44
8 Aaliyah I Don’t Wanna 4:15
9 Aaliyah Try Again 4:03
10 Adams, Yolanda Open My Heart 5:30
11 Adkins, Trace More 3:05
12 Aguilera, Christina Come On Over Baby 3:38
13 Aguilera, Christina I Turn To You 4:00
14 Aguilera, Christina What A Girl Wants 3:18
15 Alice Deejay Better Off Alone 6:50
表13：曲データセット（上）と順位データセット（下）に分けられ、正規化されたビルボードデータセット。各々のデータセットの最初の15行が示されている。曲データセットからはgenre（ジャンル）が、順位データセットからはweek（週）が割愛されている。
id date rank
1 2000-02-26 87
1 2000-03-04 82
1 2000-03-11 72
1 2000-03-18 77
1 2000-03-25 87
1 2000-04-01 94
1 2000-04-08 99
2 2000-09-02 91
2 2000-09-09 87
2 2000-09-16 92
3 2000-04-08 81
3 2000-04-15 70
3 2000-04-22 68
3 2000-04-29 67
3 2000-05-06 66

正規化は、整然化し、矛盾を排除するのに有用である。しかし、リレーショナルデータを直接扱うデータ解析ツールはほとんどないため、通常、分析では、非正規化をしたりデータセットを1つの表に統合したりすることも必要とされる。

1つの類型が複数の表にある

観測の構成単位の類型1つに関するデータ値が、複数の表や複数のファイルに散らばっていることもしばしばある。こうした表とファイルは、しばしば他の1つの変数によって分割されており、それぞれの表もしくはファイルが1つの年や1つの人を表したり、1つの場所を表したりする。個々の記録の形式が一致しているかぎり、これは修正するのが容易な問題である。

  1. ファイルを読み込んで、表のリストにする。
  2. 各表に対して、元のファイル名を記した新しい列を追加する（ファイル名が重要な変数の値であることが多いため）。
  3. すべての表を結合し、1つの表にする。

plyrパッケージを使えば、これはRにおいて何のこともない作業になる。以下のコードは、あるディレクトリ (data/) において.csvで終わるという正規表現にマッチするファイル名のベクトルを生成する。次に、ベクトルの各要素に対する名前として、元のファイル名を付ける。こうするのは、plyrが次の段階で名前を保持し、最終的なデータフレームの各行がその出所のファイルでラベル付けされていることを保証するためである。最後に、ldply() がすべてのパスに対してループを回し、CSVファイルを読み込み、結果を単一のデータフレームに結合する。

paths <- dir("data", pattern = "\\.csv$", full.names = TRUE)
names(paths) <- basename(paths)
ldply(paths, read.csv, stringsAsFactors = FALSE)

単一の表を作成しさえすれば、必要に応じて追加的な整然化を実行できる。この種のクリーニングの例として、米国社会保障庁 (US Social Security Administration) が提供する年ごとの赤ん坊の名付けに関する129個の表を1つのファイルに取りまとめたものがある。これは https://github.com/hadley/data-baby-names で手に入れることができる。

データセットの構造が徐々に変化する場合には、より複雑な状況が発生する。例えば、こうした変化があるデータセットには、異なる変数、異なる名前の同じ変数、異なるファイル形式、または欠損値に関する異なる規則が含まれる可能性がある。このため、ファイルごとに別々に整然化する必要があるかもしれない（あるいは、運が良ければ小さいグループごとということになるかもしれない）。この種の整然化の例は https://github.com/hadley/data-fuel-economy に示されている。これは、1978年から2008年までの5万台を超える米国環境保護庁の燃費データを整然化したものである。この生データはオンラインで入手できるが、年ごとに別々のファイルに格納されており、なおかつ主要な形式だけでも4種類ある上、さらに細かな差異が多数見られる。このため、このデータセットを整然化するのはかなりの難題である。

整然ツール

整然データセットを手に入れたら、それで何ができるだろうか。整然データは、それによって分析が容易になるときにかぎって、価値がある。本節では、整然データセットを入力とし、整然データセットを出力として返す整然ツール (tidy tool) について議論する。整然ツールは、1つのツールの出力が他のツールの入力として使用できるため、有用である。そして、このことにより、問題を解決するために、複数のツールを単純かつ容易に組み合わせることができるようになる。さらに、整然データは、変数が一貫した明示的な方法で格納されることを保証する。このことにより、各々のツールは単純なものになる。なぜかと言えば、異なるデータセット構造を扱うためのパラメータを含むような、スイスアーミーナイフのように1つでさまざまなことができるツールを必要としないためである。

ツールが雑然となる理由は2つある。すなわち、雑然データセットを入力として受け付ける（雑然入力ツール [messy-input tool]）か、雑然データセットを出力として生み出すか（雑然出力ツール [messy-output tool]）である。雑然入力ツールは、整然化の過程についての部分を含める必要があるため、通常、整然入力ツールより複雑になる。雑然入力ツールは、一般的な種類の雑然データセットには役立つものの、往々にして機能が複雑になり、利用と保守が困難になる。雑然出力ツールは、いらだたしいものであり、分析が遅くなる。雑然出力ツールは容易に構成できない上、ある形式から別の形式に変換する方法について常に考えなければならないためである。本節では、双方の例を見る。

次に、分析に関する3つの重要な構成要素、すなわちデータ操作、可視化、モデル化に関して、整然ツールと雑然ツールの事例を示す。Rに既存の整然ツールが多いことから、Rが提供するツールに特に焦点を当てるが、SAS (SAS Institute Inc. 2013)、SPSS (IBM Corporation 2013) 、Stata (StataCorp 2013) といった他の統計プログラミング環境についても触れる。

操作

データ操作 (data manipulation) は、変数から変数への変換（logやsqrtなど）だけでなく、集約、選別、並べ替えを含む。私の経験上、これらはデータ操作における4つの基本動詞である。

変数を参照するための一貫した手法がある場合、これらの操作はすべて簡単になる。整然データならば、こうすることができる。なぜかと言えば、整然データにおいては、個々の変数がそれ自身の列を持っているためである。

Rでは、基本パッケージのsubset()関数で選別ができる。また、基本パッケージのtransform()関数で変換ができる。これらは入力も出力も整然である。さらに、aggregate()関数でグループ単位の集約ができる。これの入力は整然である。単一の集約方法が使用されている場合は、出力も整然となる。plyrパッケージは、集約と並べ替えのために、整然なsummarize()とarrange()関数を提供している。

これら4つの動詞は、“by”（〜によって）という前置詞で修飾することができ、実際にしばしばこの修飾が行われる。グループごとに集約したり、変換したり、部分集合を取り出したりすることは、しばしば必要になる。例えば、各グループで最大のものを選んだり、繰り返されたものを平均したりすることなどがある。4つの動詞のそれぞれと by 演算子を組み合わせることで、あるデータフレームの複数の部分集合に対して同時に操作できるようになる。ほとんどのSASのPROCはBY文を持っており、これによりグループごとの操作が可能になる。そして、通常、これらの入力は整然である。Rの基本パッケージにはby()という関数があるが、これは入力こそ整然であるものの、出力は整然でない。出力がリストになるためである。plyrパッケージのddply()関数は、これに代わる整然な関数である。

複数のデータセットがある場合、他のツールが必要となる。整然データの利点は、他の整然データセットと組み合わせることが容易なことである。組み合わせに必要になるのは、共通変数をマッチさせて新しい列を追加することで動作する結合演算子 (join operator) のみである。これは、Rの基本パッケージのmerge()関数やplyrパッケージのjoin()関数で実装されている。これらの演算子を、配列に格納されたデータセットを結合する困難さと比較してみよう。こうした作業では、行列演算が使用できるようになる前に、骨の折れるような整列が必要となるのが通常である。このことにより、非常に検出しにくい誤りを起こす可能性がある。

可視化

整然な可視化ツールは、出力が視覚的なものであるため、入力が整然であることのみが求められる。ドメイン固有言語 (domain specific language) は、変数とグラフの美的特性（例：位置、サイズ、形状、色）との間の対応関係として可視化を記述できることから、整然データセットの視覚化に特に有効である。これは、グラフィックの文法 (Wilkinson 2005) やRのために特別にあつらえられた拡張版であるグラフィックのレイヤー化された文法 (Wickham 2010) の背後にある考えである。

Rのほとんどのグラフィックに関するツールは、基本パッケージのplot()関数、latticeのたぐいの図 (Sarkar 2008)、ggplot2 (Wickham 2009) を含めて、入力が整然である。また、雑然データセットを可視化するための特殊なツールがいくつか存在している。barplot(), matplot(), dotchart(), mosaicplot()のように、いくつかの基本パッケージのRの関数は、変数が複数の列に散らばっているような雑然データセットで動作する。同様に、平行座標プロット (Wegman 1990; Inselberg 1985) を使って、個々の時点が列であるような雑然データセットの時系列グラフを作成することができる。

モデル化

モデル化は本研究の原動力となっている。なぜかと言えば、ほとんどのモデル化ツールが整然データセットで最もうまく動作するためである。どの統計用の言語にも、さまざまな変数をつなぎ合わせた形でモデルを記述する手段がある。こうした手段は、応答変数を予測変数につなぎ合わせるドメイン固有言語である。

これは、整然データが回帰を計算するために内部的に使用される形式であるという意味ではない。標準的な線形代数ルーチンに簡単に投入できる数値行列を生成するために、大規模な変換が行われる。よくある変換として、切片列（1が並ぶ列）を追加すること、カテゴリ変数を複数の二値ダミー変数にすること、データをスプライン関数の適切な基底に射影することがある。

特定の種類の雑然データセットに対してモデル化関数を適用する試みがいくつかある。例えば、SASのPROC GLMでは、REPEATEDキーワードが存在する場合、方程式の応答側の複数の変数が反復測定値として解釈される。ビルボードの生データについては、整然データのrank = week * trackの代わりにwk1 - xwk76 = trackという形式のモデルを構築することができるだろう。

もう1つの興味深い例が、古典的な対応のあるt検定である。これは、データがどう格納されているかによって、2つの方法で計算できる。データが表14(a)のように格納されていれば、対応のあるt検定はxとyの差の平均に適用されるt検定に過ぎない。表14(b) のような形式で格納されていれば、variable（変数）を示す固定ダミー変数を用いた混合効果モデルを当てはめ、個々のIDにランダム切片を加えることで同等の結果を得ることができる。Rのlme4 (Bates, Maechler, Bolker, and Walker 2014) の表記法においては、これはvalue ~ variable + (1 | id)と表される。どちらの方法でデータをモデル化しても、同じ結果が得られる。これ以上の情報がなければ、どちらのデータ形式が整然であるかについて述べることはできない。xとyが左右の腕の長さを表す場合は表14(a)が整然となるし、xとyが1日目と10日目の測定値を表す場合は表14(b)が整然となる。

表14：同じ検定を行うための2つのデータセット。(a) 対応のあるt検定のためのデータ。
id x y
1 22.19 24.05
2 19.82 22.91
3 19.81 21.19
4 17.49 18.59
5 19.44 19.85
(b) 混合効果モデルのためのデータ。
id variable value
1 x 22.19
2 x 19.82
3 x 19.81
4 x 17.49
5 x 19.44
1 y 24.05
2 y 22.91
3 y 21.19
4 y 18.59
5 y 19.85

通常、モデルの入力には整然な入力が必要となるが、こうした細心の注意はモデルの出力には引き継がれない。予測や推定された係数といった出力は必ずしも整然ではない。このため、複数のモデルの結果を組み合わせることは難しくなる。例えば、Rでは、モデルの係数の表現方法のデフォルトは、推定量ごとに変数名を記録するための明示的変数を持たないため、整然ではない。代わりに、こうした情報は行名として記録されている。Rでは、行名が一意でなければならないため、多くのモデル（例：ブートストラップによる再標本化から出てくるモデルやサブグループから出てくるモデル）の係数を結合するには、重要な情報を失わないようにするための回避策が必要となる。これは解析の流れを妨げ、複数のモデルの結果を組み合わせるのを難しくする。今のところ、私はこの問題を解決するパッケージを知らない。

事例研究

以下の事例研究では、整然データと整然ツールが、操作・可視化・モデル化の間の移動を容易にし、結果としてデータ分析を容易にすることを示す。ある関数の出力を他の関数への入力として正しい形式に変換するためだけに存在しているコードを見ることは一切ない。これから、分析を行うためのRコードを示す。ここでは、コード・結果・説明をしっかりと結びつけた形で交互に示すことで、Rについてよく知らなくても、あるいは私の使った慣用的手法についてよく知らなくても、容易に理解できるように努めたつもりだ。

この事例研究では、個人を単位としたメキシコでの死亡率データを使用する。最終的な目標は、1日を範囲としたときに異常な時間的パターンが見られる死因を検出することにある。図1は、すべての死因について1時間当たりの死亡者数を示した時間的パターンである。このパターンから最も離れている疾患を検出することが目標である。

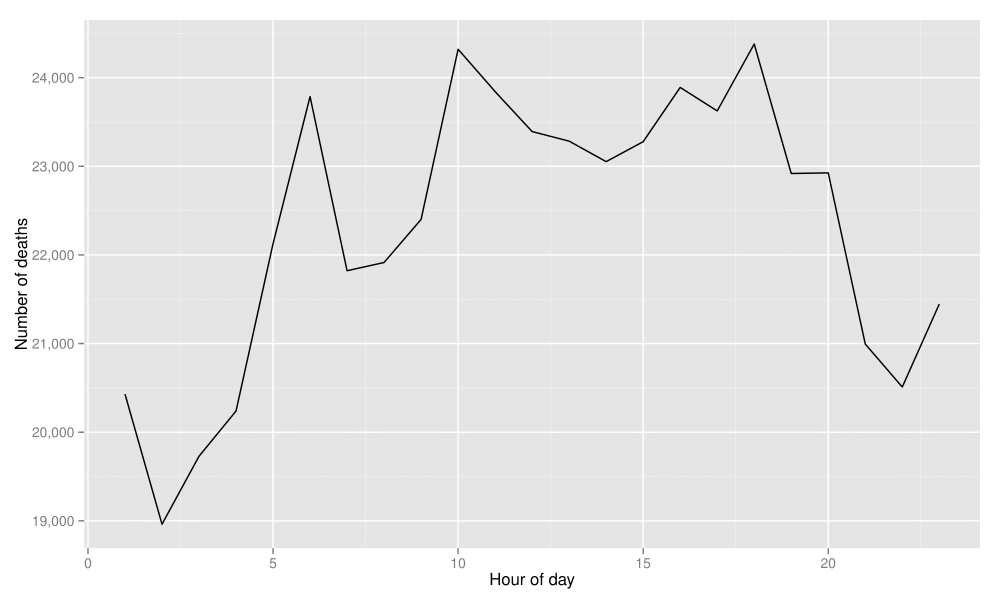
図1：すべての死因についての時間的パターン。
図1：すべての死因についての時間的パターン。

この事例研究の完全なデータセットには、2008年のメキシコにおける53万9530人の死亡に関する情報がある。そして、このデータセットには、死亡場所、死亡時間、死因、死亡者に関する人口統計学的な情報など55個の変数が含まれている。表15は、このデータセットの小規模な標本を示している。この表は、死亡時刻に関する変数（year「年」・month「月」・day「日」・hour「時」）と死因に関する変数（cod）に焦点を合わせている。

表15：53万9530行×55列の元のデータセットから、16行×5列を取り出した標本。
yod mod dod hod cod
2008 1 1 1 B20
2008 1 2 4 I67
2008 1 3 8 I50
2008 1 4 12 I50
2008 1 5 16 K70
2008 1 6 18 I21
2008 1 7 20 I21
2008 1 8 — K74
2008 1 10 5 K74
2008 1 11 9 I21
2008 1 12 15 I25
2008 1 13 20 R54
2008 1 15 2 I61
2008 1 16 7 I21
2008 1 17 13 I21

異常な時間的パターンを見つけるという目標を達成するために、以下のことを行う。まず、整然であるcount関数を用い、個々のcod（死因）についてhod（死亡の時間）ごとの死亡者数を数え上げる。

hod2 <- count(deaths, c("hod", "cod"))

次に、subsetを使って、欠損値を取り除く（欠損値は欠損しているゆえに、本事例研究の目的に対する情報価値がない）。

hod2 <- subset(hod2, !is.na(hod))

このことにより、表16(a)が得られる。次に、疾患について分かりやすいラベルを準備するために、このデータセットをcodesデータセットと結びつける。結びつけるときには、cod（死因）変数に基づいて結びつける。すると、表16(b)に示すように、新しい変数であるdisease（疾患）が付け加わる。

hod2 <- join(hod2, codes, by = "cod")
表16：データフレームのhod2から取り出した4つの疾患と4つの時間についての標本。
hod cod freq disease prop freq_all prop_all
8 B16 4 Acute hepatitis B 0.04 21915 0.04
8 E84 3 Cystic fibrosis 0.03 21915 0.04
8 I21 2205 Acute myocardial infarction 0.05 21915 0.04
8 N18 315 Chronic renal failure 0.04 21915 0.04
9 B16 7 Acute hepatitis B 0.07 22401 0.04
9 E84 1 Cystic fibrosis 0.01 22401 0.04
9 I21 2209 Acute myocardial infarction 0.05 22401 0.04
9 N18 333 Chronic renal failure 0.04 22401 0.04
10 B16 10 Acute hepatitis B 0.10 24321 0.05
10 E84 7 Cystic fibrosis 0.07 24321 0.05
10 I21 2434 Acute myocardial infarction 0.05 24321 0.05
10 N18 343 Chronic renal failure 0.04 24321 0.05
11 B16 6 Acute hepatitis B 0.06 23843 0.05
11 E84 3 Cystic fibrosis 0.03 23843 0.05
11 I21 2128 Acute myocardial infarction 0.05 23843 0.05
(a) (b) (c) (d)

死因ごとの死亡総数の違いは、何桁にもわたる。心臓発作による死亡は4万6794人であるのに対し、雪崩による死亡はわずか10人に過ぎない。ここから、総数でなく、1時間あたりの死亡率を比較することが理にかなっていることが示唆される。これは、cod（死因）でデータセットを分割し、transform()を用いて1時間あたりの頻度をその死因の総死亡数で割ったprop（比率）という新しい列を加えることで求められる。この新しい列は、表16(c)に示されている。

ddply()は、第1の引数 (hod2) を第2の引数（cod変数）で分割し、第3の引数 (transform) を分割された個々の部分に適用する。第4の引数 (prop = freq / sum(freq)) は、transform()にわたされる。

hod2 <- ddply(hod2, "cod", transform, prop = freq / sum(freq))

次に、1時間あたりの全体的な平均死亡率を計算し、元のデータセットに統合する。これにより表16(d)が得られる。prop（比率）とprop_all（全体的な比率）を比較することで、各疾患を全体の発生パターンと容易に比較することができる。

まず、1時間ごとの死亡者数を何とかしよう。hodでhod2を分割し、死因ごとに合計を計算する。

overall <- ddply(hod2, "hod", summarise, freq_all = sum(freq))

次に、1時間ごとに、全体的に見たときの死亡者の割合を計算する。

overall <- transform(overall, prop_all = freq_all / sum(freq_all))

最後に、全体的に見たデータセット (overall) を個別的に見たデータセット (hod2) と結合することで、両者を比較しやすくする。

hod2 <- join(hod2, overall, by = "hod")

次に、1つ1つの死因の時間的パターンと全体の時間的パターンとの間の距離を計算する。この距離を測定するやり方にはさまざまなものがあるが、単純平均二乗偏差 (simple mean squared deviation) が理解を助けるだろう。また、各死因について、標本の大きさ（その死因による総死亡者数）を記録する。考察対象とする疾患が十分に代表的なものであるようにするために、50人（1時間当たり約2人）を超える死亡がある疾患のみを扱うものとする。

devi <- ddply(hod2, "cod", summarise, n = sum(freq),
  dist = mean((prop - prop_all)^2))
devi <- subset(devi, n > 50)

この推定量の分散に関する特性は分からないが、図2(a)のようにn（標本の大きさ）とdeviation（偏差）を図示することで視覚的に探索することができる。線形な目盛りでは、標本の大きさが増えるにつれて散らばりが小さくなること以外、図から分かることはほとんどない。しかし、両対数目盛りにした図2(b)では、明確なパターンが見いだせる。このパターンは、頑健な線形モデルから得られた最適の当てはめ直線を追加すると特に見やすくなる。

ggplot(data = devi, aes(x = n, y = dist) + geom_point()
last_plot() + scale_x_log10() + scale_y_log10() +
  geom_smooth(method = "rlm", se = F)
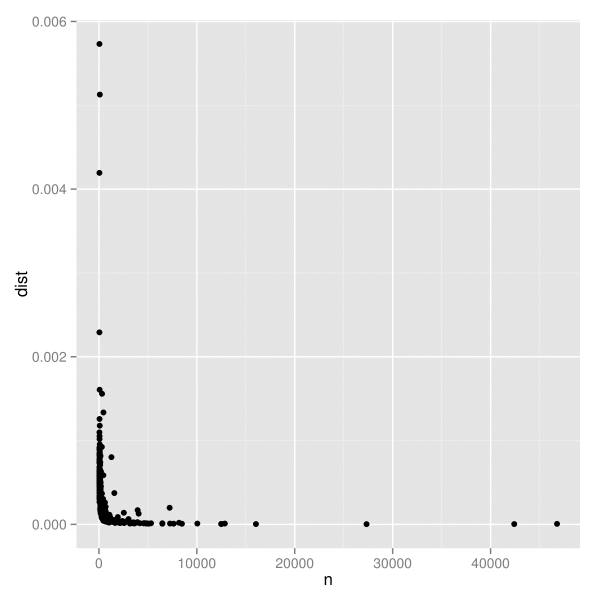
図2(a)：<code>n</code>（標本の大きさ）と<code>deviation</code>（偏差）のグラフ。偏差の散らばりは標本の大きさに大きく左右されており、標本が小さいほど散らばりが大きい。
図2(a)：n（標本の大きさ）とdeviation（偏差）のグラフ。偏差の散らばりは標本の大きさに大きく左右されており、標本が小さいほど散らばりが大きい。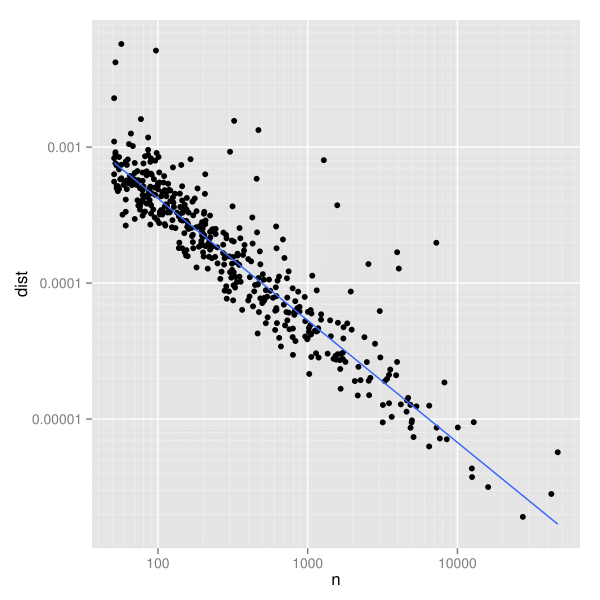
図2(b)：両対数のグラフは散らばりのパターンと異常に高い値を見いだしやすい。青線は最も当てはまりがよい頑健な直線である。
図2(b)：両対数のグラフは散らばりのパターンと異常に高い値を見いだしやすい。青線は最も当てはまりがよい頑健な直線である。
図3：log(n) から log(dist) を予測する頑健な線形モデルからの残差。1.5のところにある水平線は、さらなる探索のための閾値を示す。
図3：log(n) から log(dist) を予測する頑健な線形モデルからの残差。1.5のところにある水平線は、さらなる探索のための閾値を示す。

我々は、x軸に関して近いもの同士の中でyの値が相対的に大きいような点に関心を持っている。死亡者数を統制したとき、こうした点は全体のパターンから最もかけ離れた疾患を表す。

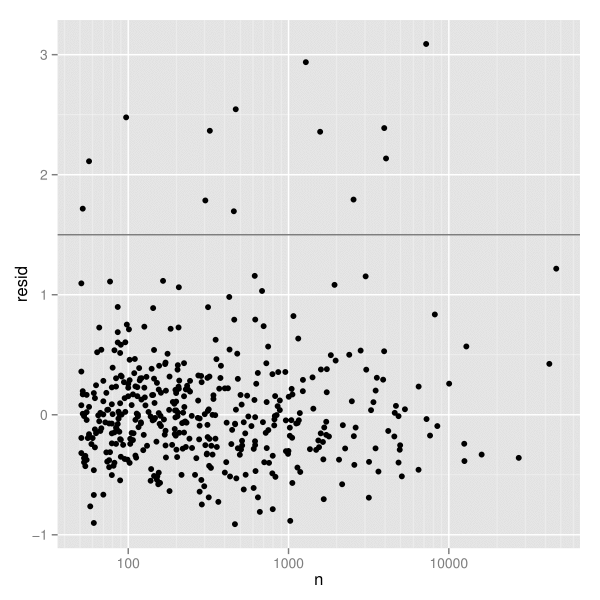
こうした異常な点を見つけるために、頑健な線形モデルを当てはめ、残差を図示する（図3）。図では残差が1.5の辺りが何もない領域となっている。このため、いささか恣意的ではあるが、残差が1.5以上になる疾患を選び出すことにする。このことは、2段階で行われる。まず、devi（疾患ごとに1行）から適切な行を選択する。そして、元の要約データセット（疾患ごとに24行）から一致する時間経過の情報を見つけ出す。

devi$resid <- resid(rlm(log(dist) ~ log(n), data = devi))
unusual <- subset(devi, resid > 1.5)
hod_unusual <- match_df(hod2, unusual)

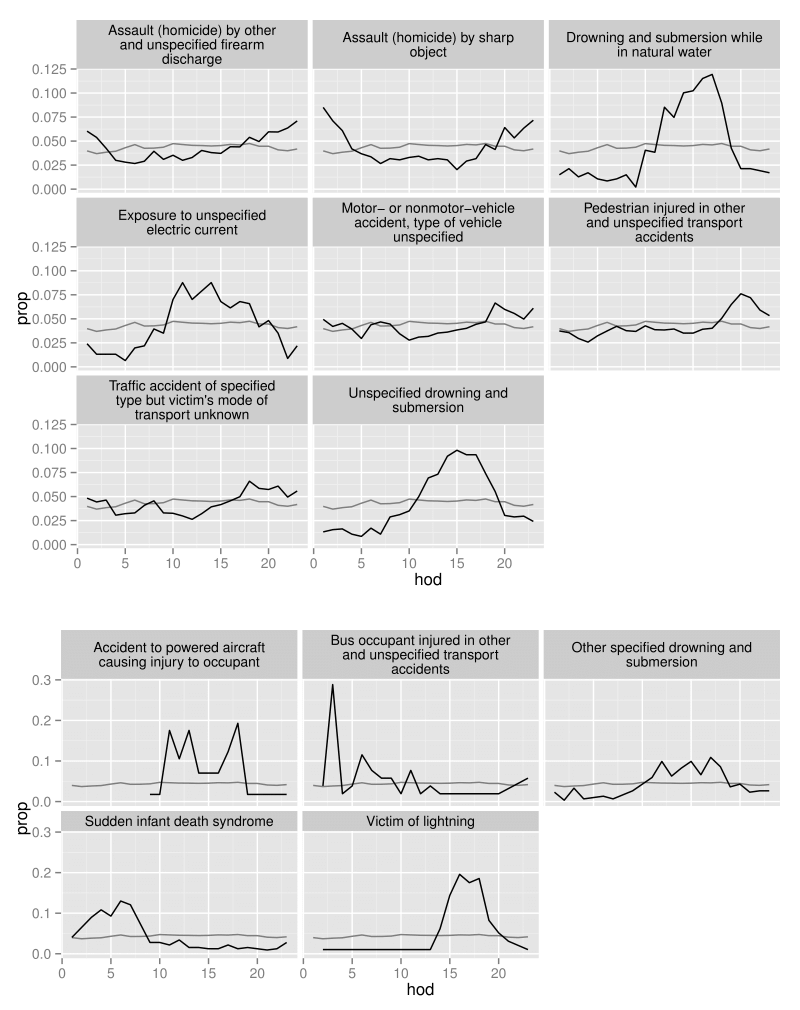
最後に、異常な死因ごとに時間的推移を図示する（図4）。ここで、変動の違いにより、疾患を2つの図に分けた。上の図は、死亡者数が350人を超える疾患を示す。これに対して、下の図は死亡者数が350人に満たない疾患を示している。死因は、殺人・溺死・交通関連の3つの主要なグループに分類される。殺人は、夜間によく見られる。溺死は午後に見られる。交通関連の死亡は、通勤時間帯に見られる。背景の薄い灰色の線は、すべての病気を通じて見たときの時間的推移を示している。

ggplot(data = subset(hod_unusual, n > 350), aes(x = hod, y = prop)) +
  geom_line(aes(y = prop_all), data = overall, colour = "grey50") +
  geom_line() + facet_wrap(~ disease, ncol = 3)
図4：異常な時間的推移が見られる死因。全体の1時間ごとの死亡率は灰色で示されている。（上側）1年で死亡者が350人を超える死因 [2] 。（下側）死亡者が350人に満たない死因 [3] 。上側と下側とでy軸の目盛りが異なることに注意。

結論

データクリーニングは重要な問題であるが、統計学の研究対象となることはあまりない。本論文は、データクリーニングにおける、小さなことではあるが重要な一部分を切り開くものである。この一部分は、すなわち、データ操作、可視化、モデル化を容易にするためのデータセットの構築であり、私はこれをデータの整然化と呼んだ。なされるべき作業はまだたくさんある。整然データと整然ツールに対する理解が向上し、データを整然な形にする際のあつれきを減らす能力が向上するにつれ、段階的に改善が行われるようになるだろう。

整然さを構成する代替的手法を探索することによって、より大きな改善が可能になるかもしれない。整然データには、ニワトリが先か卵が先かという問題がつきまとっている。整然データの有用さがそれを扱うツールの有用さを超えないのであれば、整然ツールは整然データに密接に結びついたものになるだろう。これにより、独立して変化するデータ構造またはデータツールがワークフローを改善しない場合、容易に局所的な最大値に陥ることになる。この局所的な最大値から脱出することは難しい。それには、多くの誤った開始点での見通しに対する長期的な協調した努力を必要となる。私は整然データのフレームワークがそうした誤った開始点の1つでないことを願っているが、整然データが最終的な解決策であるとも見なしていない。私は他の人がこのフレームワークに基づいて、さらに優れたデータ格納戦略やツールを開発することを願っている。

意外なことに、整然データの設計を支配する原則で、統計的および認知的要因の両方を認めるものはきわめて少数であることが見いだされた。これまでのところ、私の研究成果は、自分自身のデータ分析の経験、リレーショナルデータベース設計に関する自分自身の知識、データ分析のツールについて自分自身がなした熟考に基づいている。ヒューマンファクター（human factor, 人的要因）、ユーザー中心設計 (user-centered design)、ヒューマンコンピューターインタラクション（human-computer interaction, 人と計算機の間の相互作用）に関するコミュニティーが、この対話に加わることができるかもしれない。しかし、データの設計とそれを扱うツールの設計は、これらの分野で活発な研究課題となっていない。将来的には、データ分析の認知側の理解を向上させ、適切なツールを設計する能力をさらに向上させるために、これらの分野の方法論（ユーザーテスト [user-testing]、エスノグラフィー [ethnography]、思考発話プロトコル [talk-aloud protocol]）を使用したいと考えている。

整然データを他の方法で構成することも可能である。例えば、多次元配列に格納された値を処理するツール群を構築することが可能だろう。多次元配列は、マイクロアレイや fMRI によって生成される大規模な生物医学上のデータセットにおいて、ありふれたデータ格納フォーマットである。これは、行列操作に基づく多変量解析手法の多くにおいても必要になる。幸いなことに、疎であるものも含めて、高次元の配列を扱うための効率的なツールがたくさんあるので、配列に即して整然な形式のたぐいは、非常にコンパクトで効率的な見こみがあるだけでなく、統計の数学的な基礎と容易に結びつけることが可能なはずである。実を言うと、これは Python データ分析ライブラリである pandas (McKinney, 2010) が採用しているアプローチである。さらに興味深いことに、メモリ使用量とパフォーマンスを最適化するため、基底にあるデータ表現を無視して、配列に即して整然なフォーマットとデータフレームに即して整然なフォーマットのいずれかを自動的に選ぶ整然ツールを考えることもできるだろう。

データクリーニングにおいては、整然化のほかに、数多くの作業がある。例えば、日時や数値の構文解析 (parsing)、欠損値の特定、文字エンコーディングの修正（国際的データの場合）、類似しているが同一でない値（タイプミスで作成されたもの）をマッチさせること、実験デザインの検証、構造的な欠損値の補完、そして言うまでもなく、疑わしい値を特定するためのモデルに基づくデータクリーニングがある。我々は、これらの作業をより簡単にするための他のフレームワークを開発できるだろうか？

謝辞

本研究は、私がデータに関してなした多くの対話や、データを統計的に扱う方法についての多くの対話がなければ、可能とはならなかっただろう。 長年にわたって数多くの質問に我慢してくれた Phil Dixon, Di Cook, Heike Hofmann に特に感謝したい。 挑戦的な問題をたくさん出してくれたreshapeパッケージのユーザーと、私が知っていることを学生が理解できる形で説明するという挑戦を続けさせてくれた私の学生にも感謝したい。早い段階の草稿に対して詳細なコメントをくれた Bob Muenchen, Burt Gunter, Nick Horton, Garrett Grolemund にも感謝したい。また、変数を定義するという挑戦に対してすばらしい事例を示してくれた Ross Gayler と、対応ありのt検定と混合効果モデルとの自然同値性について教えてくれた Ben Bolker にも特に感謝したい。

参考文献

脚注
  1. 原注：http://religions.pewforum.org/pdf/comparison-Income%20Distribution%20of%20Religious%20Traditions.pdf [↩]
  2. 訳注：上側における死因を和訳すると以下の通りになる。（上側の上段）左から順に、「その他及び詳細不明の銃器の発射による加害にもとづく傷害及び死亡」、「鋭利な物体による加害にもとづく傷害及び死亡」、「自然の水域内での溺死及び溺水」。（上側の中段）左から順に、「詳細不明の電流への曝露」、「車両（駆動形態を問わない）事故、車両の型式不明」、「その他及び詳細不明の交通事故により受傷した歩行者」。（上側の下段）左から順に「事故の形態が明示され、受傷者の輸送形態が不明の路上交通事故」、「詳細不明の溺死及び溺水」。なお、この事例研究における死因は、国際疾病分類第10版 (ICD-10) と呼ばれる分類に従っている。死因の和訳は標準病名マスター作業班が提供している ICD-10 の和訳によった。 [↩]
  3. 訳注：下側における死因を和訳すると以下の通りになる。（下側の上段）左から順に、「乗員が受傷した動力航空機事故」、「その他及び詳細不明の交通事故により受傷したバス乗員」、「その他の明示された溺死及び溺水」。（下側の下段）左から順に「乳幼児突然死症候群」、「落雷による受傷者」。 [↩]