はじめに
言語研究者になろうとしている人が、統計を勉強する場合、どうやって勉強すれば良いかについて簡単に紹介したいと思う。今回は、統計の基礎を身につけることに重点を置きたいと思う。より応用的なことについては、また別の記事で書きたいと思う。(2011年6月28日追記:「言語研究者のための統計の学び方―より高度な内容」というタイトルで公開済み。)
言語研究者が統計を勉強する場合、単に統計学の教科書を読めば良いというわけではない。実際に統計を言語研究に適用する段になると、言語研究特有の取り扱いをしなくてはならないことがどうしても出てくる。一般的な統計学の教科書は、言語研究者のために書かれているわけではないので、言語現象特有の取り扱いについては触れられていない。このため、単に統計の知識を入れるだけでなく、それを言語研究にどう生かしていくかという視点を持ちながら勉強していくことが重要になる。
この記事の対象読者
この記事の対象読者としては、言語学などの言語研究をしている学科に所属している大学3-4年生 [1] ぐらいを想定している。特に将来的に大学院に進学して研究を続けたいという人向けに書かれている。もちろん、進学しない人でも、卒論で統計を使う場合には、この記事の内容が活用できると思う。
統計に関する知識は全くゼロで構わない。ただ、言語学の入門講義などを受けて、言語研究で大体どのようなことが行われるかは分かっていた方が望ましい。統計が言語研究とどう関わってくるかについては、先日、「言語研究と統計の関係」という記事を書いたのでそれを参照して欲しい。
本当に統計を学ばないといけないのか?
この記事を読んでくれている時点で、統計にはある程度の関心を持ってくれているのだと思うが、一応、本当に統計を学ばなくてはならないのかについて考えてみたいと思う。
統計を使わない言語研究をする人は?
言語研究の中には、あまり統計を使わない分野もある。こういった分野を研究するのならば、直接的には統計は必要ない。だが、自分が使わないとしても、隣接分野の研究で統計が用いられるうるので、やはり統計は理解していた方が良いと私は思う。
コンピュータに任せれば良いのでは?
今は、「お手軽に」統計が扱えるツールが簡単に手に入る。こういったツールを使うと、統計を知らない人でも、統計処理めいたことができる。しかし、統計をしっかり理解していない場合、見るに堪えない結果が出てくることが多い。こういったツールを使う場合でも、色々な選択を行わなくてはならないのだが、統計を知らない場合、間違った選択を行ってしまうことが少なくない。
例えば、以下のようなデータが与えられたとしよう。これは、中学校の英語の授業で、各学年の修了時までに何単語勉強するかを示した表である。中1で512単語勉強して、さらに中2で311単語勉強するので、中2修了時では合計で823単語になるという寸法だ。
| 学年 | 語彙数 |
|---|---|
| 中学1年生 | 512 |
| 中学2年生 | 823 |
| 中学3年生 | 1061 |
この表をExcelやOpenoffice.org Calcといった表計算ソフトでグラフにすることを考えてみよう。表計算ソフトでは、簡単にグラフを作ることができるが、そこでも色々な選択を行う必要が出てくる。例えば、下図のようにグラフの種類を選ばなくてはならない。
どのようなグラフを選べば良いかは、表計算ソフトは教えてくれないので、自分で考える必要がある。ちゃんと選択すれば、とても良いグラフを作ることができるが、選択を誤ると、不適切な出力が出てきてしまう。次に掲げる円グラフは、不適切なグラフを出力してしまった例である。
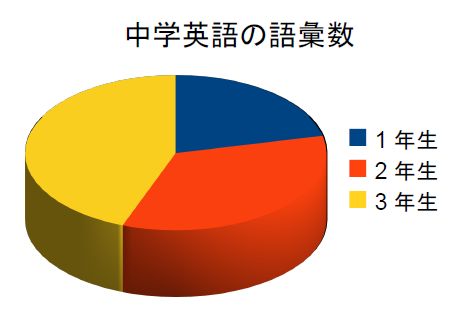
人によってはこのグラフを見て、「全く意味が分からない、どうしよう」と思うかもしれないが、心配することはない。この円グラフ [2] は全く意味をなさないグラフである。円グラフは、そもそも全体に占める割合を表すためのグラフである。ここで扱っているデータはそもそも割合を扱っているわけではないので、円グラフを使うことは不適当である。
なお、以下のように棒グラフにすると、ぐんと良くなる。
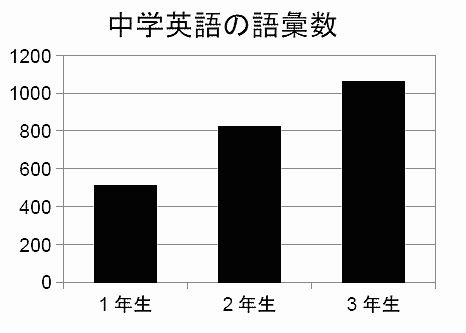
今の例はいかにも馬鹿げた例だけれども、もっと分かりづらい罠は、あちこちに存在している。そういった罠に引っかからないためにも、しっかり統計を勉強しておく必要があるのだ [3] 。
なお、お手軽な統計ツールを使うこと自体は悪いことではない。ただし、統計をしっかり理解しているという前提のもとで使うべきだ。たとえて言えば、年端の行かぬ子どもが火を使うのは問題があるが、分別のある大人が自己の責任の下で火を使うのは問題ないということだ。
言語研究を志す者はどう統計を勉強すれば良いか?
今まで書いてきたことで、言語研究をしようとしている人は統計を勉強した方が良いということが分かってもらえたと思う。それでは、具体的にどう勉強すれば良いのだろうか?
一番良いのは、言語研究と統計の両方に精通した教師を見つけることである。自分の興味分野と同じ専門だったら、なおのこと良い。そういった教師について勉強していくのが一番である。自分で統計を使っていて分からないことがあったら質問することもできる。ただ、実際には、そういった教師に巡り会える可能性は少ない。
本当は、教育カリキュラムの中に、言語研究における統計の利用法についての授業があるのが良いのだが、そういった場合もかなり少ない [4] 。特に言語学系の学科ではそういった授業を受けられる機会はなかなかないだろう [5] 。
となると、いきおい、自助努力に頼らざるを得なくなる。自己責任で勉強しなくてはならないのだ。自分で教科書を見つけて、自習していくことになる。1人でやるのは心配だという人は、仲間を見つけて一緒に勉強するのも楽しいと思う。自分の学科にいる人でも良いし、 Twitter や Facebook などのソーシャルネットワークサービスを活用して仲間をさがすという手もあるだろう。具体的にどのような教科書を使えば良いかは、以下で紹介するので、参考にしてほしい。
学習の順序について
私が思うに、以下の順序で統計を学習していくのが効率的だと思う。他の人には、他の人の意見があるかもしれない。あくまでもこれは独断である。
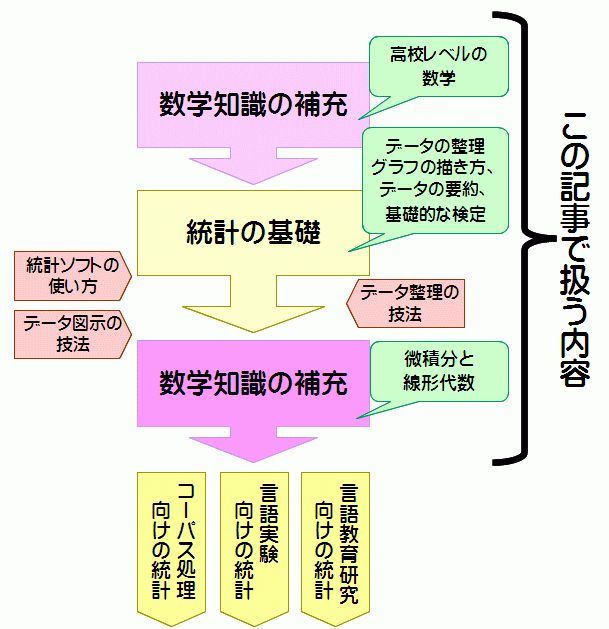
上の図は、全く統計を知らない読者が、統計を学習する際の順序を示したものである。上から順に勉強していって、最後には図の一番下まで至る。今回の記事では、この図の前半部分について説明する。後半部分は、後日説明する予定である。
まず、数学の知識をしっかり把握しておくことが重要である。統計にはどうしても数学の知識が必要となるからだ。もっとも最初から難しい数学を勉強する必要はない。最初は高校レベルの内容で十分だ。
次に、基礎的な統計を勉強する。何が基礎的かということは、人によって基準が違うと思うが、この記事の後のほうに書いてあるので参照して欲しい。この基礎的な統計が把握さえできれば、卒論程度なら十分役に立つ [6] 。
基礎的な統計を勉強したら、統計ソフトの使い方など、周辺的な内容を把握しておく必要がある。その後、次のステップに進むために、もう一度数学をしっかり勉強しておいた方が良いだろう。
最後の段階は、3つのルートに分けて描いた。これは、先日、「言語研究と統計の関係」という記事で述べたように、言語研究と統計の関わり方には様々なものがあるから、自分の研究方向に応じて、勉強する内容が変わってくるということを示している。
数学を勉強しておこう
統計学には、数学の知識が必須である。しかし、言語研究を志す学生は、数学が必ずしも得意でない。こういった学生が所属する学科は文学部や外国語学部といったいわゆる「文系」の学部の場合が多いと思う。こういった学部では入試に数学がない場合も多いし、入学後に数学に触れる機会も少ないだろう。また学生自身も「自分は文系だから」と考えて数学に苦手意識を持っている場合が多い。
このため、統計の勉強を始める前に、数学をしっかり勉強しておくと良い。数学を勉強するというと何だか大変そうだと身構えてしまうかもしれないが、とりあえずは、高校1年生程度の数学の内容が分かっていれば良い。この程度の内容なら、大学入学以前にどこかで学んだことがあると思うので、ほとんどの人にとっては復習ということになると思う。「自分は数学が苦手だから」と考えて、数学を避けるのではなく、積極的に取り組んでいきたい。
数式が出てくると分かりづらい?
「数式が出てくると分かりづらい」と考えてしまう人は少なくない。しかし、このような考えは誤りである。実際には、数式を用いることで、普通の言葉では説明しづらいことを分かりやすく示すことができるのだ。数式は、別に読者を混乱させるために存在しているのではない。もし数式が分かりづらいと思うのならば、それは数式に対する予備知識が足りないだけのことである。しっかり数学を学びさえすれば、決して分かりづらいものではない。
統計の入門書のたぐいで、「数式が出てこない」ことを宣伝文句としている場合がある。こういった書籍で統計を学ぶと、結局、なぜそうなるのかということが理解できないまま終わってしまうおそれがある。また、数式がなければ、統計処理の部分がブラックボックスと化してしまう。すべてのことを完全に理解することは難しいが、最初から全く避けてしまうのは研究者の態度として問題がある。やはり、しっかりと数学的知識を蓄積した上で、統計を理解していく必要がある。
最初に学んでおくべきこと
最初に学んでおくべきことは、高校程度の数学だ。それほどハイレベルなことをやる必要はない。大体が高1レベルの数学で何とかなる。どの時期に高校に通っていたかにもよるが、「数学I」・「数学A」の内容に、「数学II」・「数学B」を若干加えた程度の知識があれば、十分だと思う。
実際に学ぶときは、高校の数学の教科書を使えば良いだろう。自分が高校の頃、使っていたものでOKだ。高い参考書や問題集は必要ない。もしも、高校の教科書を捨ててしまったとか、そもそも高校に通っていたのが十数年前だという人は、市販の数学書で、高校程度の内容を扱っている本は色々あるので、書店などに行って、自分の肌に合った本を買えば良い。できれば、簡単な練習問題が付いている本を買って、実際に問題を解いてみるのが良い。
例えば、『もういちど読む数研の高校数学 第1巻』という、高校の数学の教科書を再編集した書籍も市販されている。ただ、この本は、練習問題の解説が付いていないので、あまりおすすめはできない。
学んでおいた方が良い内容を挙げると、次のようになるだろう。微積分や行列はとりあえず [7] 学ばなくて良い。図形や幾何に関することも特に学ぶ必要はない。
- 文字式の取り扱い
- 総和
- 組み合わせ論
- 確率
- 対数
以前、私が統計の基礎の勉強会をやったときは、統計の内容に入る前に、こういった基礎的な数学を先に学習することにした。効果のほどはわからないが、あらかじめこういった数学の知識を補充しておいたことで、後の統計の理解が少しは良くなったと思う。
文字式の取り扱い
文字式の取り扱いと言っても、複雑なことを覚える必要はない。x とか y が出てきたときに、「ぎゃー、もうやだー」とか言わないように慣れることが大事。
あとは、ギリシャ文字の読み方を覚えておくと良い。言語学だと、術語の中にたまにギリシャ文字が出てくることがある割に、ギリシャ文字の読み方を知らない人が結構いたりする。統計でよく使うギリシャ文字を以下に挙げておく。
| 読み方 | ローマ字転写 | 大小 | 主な用途 | |
|---|---|---|---|---|
| α | アルファ | alpha | 小文字 | 有意水準 |
| β | ベータ | beta | 小文字 | (1-β)で検出力 |
| Γ | ガンマ | gamma | 大文字 | Γ函数 |
| θ | シータ | theta | 小文字 | 確率分布を示すパラメータ |
| λ | ラムダ | lambda | 小文字 | ポアソン分布のパラメータ |
| μ | ミュー | mu | 小文字 | 母集団での平均 |
| ρ | ロー | rho | 小文字 | 母集団での相関係数 |
| π | パイ | pi | 小文字 | 円周率 |
| Σ | シグマ | sigma | 大文字 | 総和記号 |
| σ | シグマ | sigma | 小文字 | 母集団の標準偏差 |
| Φ | ファイ | phi | 大文字 | 正規分布の累積分布函数 |
| φ | ファイ | phi | 小文字 | 正規分布の確率密度函数 |
| χ | カイ | chi | 小文字 | χ2分布という確率分布 |
総和
総和と言っても、ピンと来ない人もいる。要するに与えられた規則に基づいて、数を足していくだけの話なのだけれども、慣れないとどういったものだか分かりづらいところがある。
総和記号の使用例
\[
\sum_{n=3}^{7} 2i = 2 \cdot 3 + 2 \cdot 4 + 2 \cdot 5 + 2 \cdot 6 + 2 \cdot 7
\]
いずれにせよ、統計の教科書では、総和の記号がよく出てくるので、総和記号の取り扱いに把握しておくと統計が理解しやすくなる。高校の教科書だと、普通、数列について扱っている章に載っている。
組み合わせ論と確率
組み合わせ論と確率については、統計の入門書にもしっかり載っているので、特に力を入れる必要はないと思う。「そう言えばこんな感じなのだな」と、軽く確認するだけで十分だ。
対数
言語現象は対数の形で表されることが多いので、しっかり把握しておくことが重要である。
統計の基礎を勉強し終わった後に学ぶべきこと
今まで述べてきたのは、統計の基礎を学ぶ前に学ぶべき数学の知識だった。ごく基礎的な統計学を理解するのなら、これで十分だ。
しかし、もう一歩進んで、中級レベル、具体的には一般(化)線形モデルであるとか多変量解析であるといった複雑な統計手法を使う場合、もうちょっと数学を勉強しておく必要がある。具体的には、微積分と線形代数を理解していおく必要がある。数学が苦手な人にとっては、大変なところではあると思うが、しっかり数学を勉強しておけば、後の学習が楽になる。

なお、微積分や線形代数の知識がなくても、何とかなると言えば何とかなる。だが、統計の勉強が進めば進むほど、微積分や線形代数の知識がないと困ってしまう。最初は楽だけれども、後で大変になるということだ。

私としては、統計の基礎を終えた段階で、微積分と線形代数を一通り勉強しておくことをおすすめする。何せ、後で複雑な統計手法を勉強するときに、ぐんと楽になるので。それほど細かく理解している必要はなく、肝心なところだけ把握しておき、必要になったらいつでも見直せるようにしておけば良い。
具体的にどう学べば良いか
多くの大学では、主に理系の1-2年生向けに、微積分と線形代数の入門講義が行われているので、大学生ならそういった授業に出るという方法がある。
何か教科書を買ってきて自習するという方法もある。微積分と線形代数が両方載っている教科書は普通ないので、それぞれで1冊ずつ用意する必要があるだろう。色々な教科書が出ているので、大きな書店で自分の肌に合った本を選べば良いと思う。演習問題とその解説がちゃんと付いている本なら、自習には使いやすいだろう。理系の友達に、おすすめの本がないか聞いてみるのも良いかもしれない。

一例として『オイラーの贈物』という本がある。この本は、微積分の基礎的な内容 [8] を丁寧に説明している。
統計の基礎を知るには
さて、前置きが長くなってしまった。本題の統計の学習について、紹介することにしよう。
準備しておくべき物は以下の通り。勉強し始める前に、持ち物が足りていないか確認しよう。
私が考えている統計の基礎とは、以下のようなことだ。後に挙げる教科書などを使えば、この辺のことが大体分かるようになる。
- データの整理:与えられたデータを処理しやすい形に変える
- データの図示:与えられたデータをグラフにする
- データの要約:与えられたデータの平均やちらばりの具合を計算する
- 基礎的な検定:2つのグループを比較する
2つのグループを比較する手法は、地味だが有用である。これで結構いろいろなことができるのだ。

2つのグループは色々設定することが可能だ。例えば、男と女という性別の違いや、関東と関西という地域の違いなどが設定できる。これを研究につなげることも容易だ。例えば、「ら抜き言葉」という言語現象があるが、東京の山の手と下町とで、どちらのほうが「ら抜き」が多いのかということを調べることが考えられる。これだけでも、立派な研究ができる。卒論程度ならばこれで十分書けるはずだ。
統計を全然知らない人にとっては、何のことだか分からないかもしれないが、統計の基礎を学習する段階で把握しておくべき術語をいくつか挙げておこう。統計の基礎が分かるようになったら、この辺の用語の意味がちゃんとわかるようになっているはずだ。
- 母集団・標本
- 無作為抽出
- 尺度水準
- ヒストグラム
- 平均
- メディアン
- 分散・標準偏差
- 相関係数
- ポアソン分布・正規分布
- 推定・検定
- 第一種の過誤・第二種の過誤
- t検定
- χ2検定
言語研究者向けの統計の基礎の教科書
統計の一般的な入門書は多い。だが、先に述べたように、言語研究をしていると、特有の取り扱いをしなくてはならない場合が出てくる。一般的な入門書では、そういった話が出てこないので、言語研究者向けに書かれた教科書を使うのが良い。
Statistics in Language Studies
私のおすすめは、Anthony Woods, Paul Fletcher, Arthur Hughes の3人が1986年に書いた Statistics in Language Studies という本である。

- Woods, A., Fletcher, P. & Hughes, A. (1986). Statistics in Language Studies
. Cambridge University Press. (ISBN: 0521273129.)
「言語研究における統計」というタイトルの通り、言語研究者向けに書かれた書籍である。統計の前提知識は全く必要ない。この本はかなり古い本だが、今でも有用である。この本をこなせば、統計の基礎はしっかり身につけられる。なお、この本は、全部読む必要はない。前半、すなわち第1章から第11章まで読めば十分である。後半の第12章から第15章は、高度な内容である し、この本でも軽く紹介するにとどめているので、敢えてこの本を使って学ぶ必要はない。もし、気が向いたら、こういうことも行われているのだなということを知るために、さらっと読んでみても良いが。
英語で書かれているが、非常に平易なので、読む際に苦労することはないはず。むしろこれで苦労していたら、言語研究に関する論文を読めないことになってしまう。論文が読めなかったら、研究者としてはやっていけないわけだから、非常にまずい。
さて、この本で繰り返し説かれているのは、統計的な意味づけと言語研究における意味づけに違いが生じるということだ。統計学的に問題がなかったとしても、言語研究としては問題があるということがあるのだ。統計的に有意であるとか相関があるとか出てきても、それは言語研究的に有意であるとか因果関係があるとかいうことを示すものであるとは限らないのだ。
例えば、7.5.2節では、データをどう収集するかという話があり、子どもの発話の中でどれだけ現在完了形が用いられるかを調査する事例が挙げられている。一番単純な手法は、子どもの発話を順に見ていって、現在完了形になっているか調べるという方法である。だが、この本ではそういった方法は良くないと言われている。よく考えてみると、連続する発話においては、同じ時制を用い続ける可能性が高い。例えば、過去のことがテーマになっているのならば、ずっと過去形を使うだろう。だから、最初から順々に見ていくと、どうしても偏りが出てきてしまう。これを防ぐために、この本では、5発話ごとにデータを取ってみれば偏りを防ぐことができると説明している。5発話ごとということにすれば、データの収集もそれほど大変にならないし、偏りを防ぐこともできる。この本は、こういった言語研究の実務におけるこまごまとしたことにも触れられているのである。
なお、この本は、コンピュータでどうやって統計を計算するのかについては、特に触れられていない [12] 。もっとも、この本に載っていることの大体は、手計算+電卓でできる。むしろ、最初は練習だと思って、コンピュータに頼らず、手計算をしてたほうが、統計の原理が身につきやすいと私は思う。
その他の教科書(言語研究と関わるもの)
基本的には、上述の Statistics in Language Studies をしっかり勉強すれば、統計の基礎はしっかり身につくので、他の教科書は別に読まなくて良い。何冊も教科書を読むとなると、時間的な負担も大きいし、どうしても同じことの繰り返しになってしまって得られるものも少ない。だが、この際、他の教科書も紹介しておこうと思う。
まずは、言語研究者向けに書かれた教科書を挙げよう。
1冊目は、Keith Johnsonの書いたQuantitative Methods in Linguistics という本だ。

Rという統計処理ソフトの使い方が書かれているのが重要。Rの使い方を覚えたいのなら、この本を使ってみても良いかもしれない。Statistics in Language Studies と同じで、後半は難しい。とりあえず3章まで読んでおけばOK。この本は Statistics in Language Studies と比べるとかなりペースが早い。この1冊だけで統計を勉強するのは難しいと思う。また、この本は図表の作りかたがあまり書かれていないので良くない。
もう1冊、Stefan Th. Gries の書いた Statistics for Linguistics with R
という本を挙げる。

自分はこの本をちゃんと読んでいないのだが、内容的には、Quantitative Methods in Linguistics より簡単だと思う。タイトルに書いてある通り、統計処理ソフトのRを使って統計分析を行っている。第5章は、分散分析というやや高度な内容を扱っているので、基礎を勉強している人はまだ読まない方が良い。
その他の教科書(言語研究とは関係ないもの)
言語研究者向けに書かれたわけではなく、より一般向けの統計の教科書も紹介しておこう。
一般向けの統計の教科書は、本当に色々なものがある。日本語で書かれたものもあるし、英語で書かれたものもある。レベルの高いものもあれば、レベルの低いものもある。正直言って、デタラメな本もあるのだ。
私の読んだことがある本から、いくつか挙げておこう。

- 高橋 信 (2004). 『マンガでわかる統計学
』東京:オーム社.

- Takahashi, S. (2008). The Manga Guide to Statistics
. No Starch Press.
『マンガでわかる統計学』は、表題の通りマンガで描かれている。だが、基礎をしっかり丁寧に説明しており、勉強になると思う。日本語で書かれた統計の本を何か一冊読みたいというのであれば、この一冊がおすすめ。なお、The Manga Guide to Statistics というタイトルの英訳もある。2011年6月24日現在、amazon.co.jp では、英語版の方が安い。

- Dalgaard, P. (2008). Introductory Statistics with R
, 2nd eds. Springer.
Dalgaardの著書は、統計ソフトRの使い方を中心とした統計の入門書である。入門的なところからかなり高度なところまで一括して扱っている。説明は丁寧。理論的なことはあまり触れられていない。第1版の和訳として『Rによる医療統計学』というタイトルの書籍が出版されている。「医療」とついているが、医療のために統計を使う人でなくても使える。

- 東京大学教養学部統計学教室〔編〕 (1991). 『統計学入門
』東京:東京大学出版会.
上記の東大が編んだ教科書は、かなり難しいが、数理的背景が他の入門書に比べてしっかりと述べられている。数学が好きな人は読んでも良いかもしれない。
基礎を学び終えた後に補充すべきこと
先に述べた Statistics in Language Studies などを使って、統計の基礎を学び終えたとしよう。その後には何をするべきだろうか。
将来的にはもっと難しい統計的手法にチャレンジするべきだと思うが、その前にいろいろと知識を補充しておいた方が良い。次の段階に進む前に、基礎をしっかりと打ち立ててほしいということだ。また、Statistics in Language Studies は良い本なのだけれども、統計ソフトの使い方などが触れられていないので、そういった足りない点を補う必要が出てくる。
具体的には、以下の3点を補充しておくべきである。
- 統計ソフトの使用法
- データの整理方法
- データを図示する方法
統計ソフトとして何を用いるべきかを決める
手計算や電卓で統計的な計算を行うのは現実的ではない。またグラフを描くにしても手描きではいろいろと面倒である [13] 。実際の研究にあたっては、何らかのコンピュータソフトを使う必要が出てくる。
統計処理に使えるソフトは様々なものがある。代表的なものとして、R, SPSS, SAS などがあるが、特に理由がなければ、Rを使うことをおすすめする [14] 。SPSS や SAS はかなり高価な商業製品なので、学生に取って入手しづらいだろう。その点、R は費用がかからない。また、R にはさまざまな追加パッケージが用意されており、言語研究にも活用できる。
R の教科書には様々なものがあるし、ウェブ上にも様々な情報がある。それらを見て、R の基本的な使い方を覚えておくと良い。可能ならば、Statistics in Language Studies に載っている例を R ではどう処理できるかを試してみると勉強になるだろう。
Rの参考書・参考ウェブサイト
Rに関する参考書・参考ウェブサイトを挙げておこう。
- 青木 繁伸 (2009). 『Rによる統計解析
』東京:オーム社.
- 舟尾 暢男 (2009). 『The R Tips―データ解析環境Rの基本技・グラフィックス活用集(第2版)
』 東京:オーム社.
- R による統計処理 (by 青木 繁伸)
- R-tips (by 舟尾 暢男)
- RjpWiki
青木の書籍は、Rの初歩から細かく書かれており、リファレンスとしても有用である。
WebサイトR-tipsは、リファレンスとして使いやすい。ただし、統計の理論についてはあまり書かれていないので、それは別を当たる必要がある。このサイトの内容はPDFとしても提供されている。同名の舟尾の書籍は、このWebサイトR-tips の内容をまとめたものである。
RjpWiki は、Rに関する様々な情報が掲載されたWikiである。上記の参考書・参考サイトを見ても分からなかったら、ここを調べてみると良いだろう。ただし、一部の内容はかなり高度なことが書かれており、基礎を終えたばかりの人にとっては難しいかもしれない。
先に述べた、Dalgaard の Introductory Statistics with R なども、Rの教科書として使える。
Excel は使うな
なお、「統計処理に Excel を使うのはどうですか」とよく聞かれるのだが、統計処理ソフトとして Excel を使うことはおすすめしない。理由は色々あるが、Excel だけでは複雑な計算がやりづらいというのがもっと大きな理由だ。
データをどう整理するかを知る
統計ソフトとして何を使うかとも関連して、データをどう整理するかも重要になってくる。端的に言えば、コンピュータに読み込みやすい形にデータを整理する必要が出てくる。
このことについては、私は良い教科書を知らない。一番良いのは、研究室の先輩などにどういう方法でデータを集計しているかを教えてもらうことだ。
データをどう効果的に図示するかを知る
統計の基礎を学んだ後だと、統計的検定で何でもできるような気がしてしまうかもしれない。そして、統計的検定のために色々と計算をすることが、統計で一番大事なことだと思ってしまうかもしれない。実際に、多くの統計の教科書では、検定の方法にかなりのページを割いている。
検定ももちろん大事だが、ほかにも重要なことがある。データをどう図示するかである。具体的にはどうグラフを作るかということだ。統計の入門書では、こういったことが意外とちゃんと述べられていない。
Edward R. Tufte や William S. Cleveland、そして Stephen M. Kosslyn といった人たちが、グラフの描き方について本を書いているので、参考にしてみると良いかもしれない。
その他
あとは、基礎が終わった段階で、自分で言語研究に関する仮説を設定してみて、それに統計処理をかけてみると良い。習うより慣れろである。
補遺
統計のより応用的な内容の学習法については、近日、記事としてまとめる予定である。(2011年6月28日追記:「言語研究者のための統計の学び方―より高度な内容」というタイトルで公開済み。)
- もちろん、大学院生や、すでに研究者として独り立ちしている人が読んでもらっても構わない。 [↩]
- なお、この円グラフは3D化しているという点でも問題をはらんでいる。基本的にどんなグラフでも3D化することはさけるべきである。 [↩]
- 「グラフの描き方って、統計の問題なの?」と疑問に思う人もいるかもしれない。だが、データをどう表示するかは、統計手法の中でもとても重要な問題である。 [↩]
- ただし、自然言語処理に関する学科に所属している場合は、統計の利用法についての授業が多分ある。また、心理学系の学科に所属している場合は、実験計画法といった名前の授業が用意されていて、そこで統計を教えてくれる場合もある。 [↩]
- 北米に留学した人の話を聞くと、言語統計に関する授業が必修として指定されている場合が少なくない。もっとも、北米の大学院などは、コースワークがものすごく多いのだけれども、 [↩]
- 修論レベルだと、もっと複雑な統計的知識を持っている必要があるだろう。 [↩]
- 統計でもっと複雑なことをやろうとする場合、微積分や行列の知識も必要になってくる。だが、統計の基礎を学ぶときは、さしあたり微積分などの知識はなくても何とかなる。 [↩]
- 線形代数の話もほんの少しだけある。 [↩]
- 先に述べたように、統計の基礎に取りかかる段階では、数学の高度な知識は要らない。微積分や線形代数が分からなくても構わない。 [↩]
- 言語学に関する入門講義などをしっかり受けていると仮定。 [↩]
- これから紹介する本は英語の本ばかりなので、英語が読めないと困る。 [↩]
- 正確に言えば、Minitabという統計ソフトの使用法が触れられているのだが、さすがに25年前の使用法を見ても役に立たない。 [↩]
- もっとも、統計の基礎を勉強する段階では、練習として手でやってみると、理解に役立つと思う。 [↩]
- 「特に理由がある」場合には、例えば、研究室の他の人がみな SPSS を使っている場合がある。こういった場合、研究に関するリソースも SPSS で使いやすいように用意されているだろうし、他の人とデータをやり取りするときも SPSS を使うことが前提になっているだろうから、SPSS を使えば良い。 [↩]