一定の方位・距離にある地点の計算
このパッケージの今までの紹介記事として以下のものがある。
R の geoshpere パッケージでは、destPoint() という函数を用いて、ある地点から一定の方位・距離にある地点の経度・緯度を求めることができる。この函数は、destPoint(p, b, d)という形で用いる。ここで、p は基準点の位置(経度・緯度)、b は方位、d は距離である。方位は真東が90度、真北が0度、真西が-90度、真南が-180度となる角度で示す。また、距離はメートルで示す。
例えば、東京駅(東経139.766905度、北緯35.681242度)から北東を向いて80キロメートルの地点はどこか知りたいとしよう。北東方向は45度、80キロメートルは80000メートルに相当するから、以下のように計算すればよい。
library("geosphere")
tokyo <- c(139.766905, 35.681242)
destPoint(tokyo, 45, 80000)
すると、以下の結果が得られ、東経140.3958度、北緯36.18942度の地点が答えであることが分かる。これは茨城空港の付近に位置する地点である。
lon lat
[1,] 140.3958 36.18942
応用1:東京から真西を向いた先には何があるか?
東京から真西を向いた先には何があるだろうか。destPoint()函数を使って調べてみよう。東京から真西に0, 1000, 2000, …, 30000キロメートルの位置を計算して、それを地図上に表してみよう。真西は-90度と表される。そして、0, 1000, 2000, …, 30000キロメートルを示すベクトルとして0:30*1000000を組み合わせる。なお、geoshpere パッケージでは距離をメートルで表すことに注意。
# 東京の位置 tokyo <- c(139.766905, 35.681242) # 東京から真西に1000キロメートルずつの位置を計算 west <- destPoint(tokyo, -90, 0:30*1000000) # 世界地図の描画 data(wrld) plot(wrld, type = "l") # 東京から真西を向いた方向の線を書き加える lines(west, col = "red")
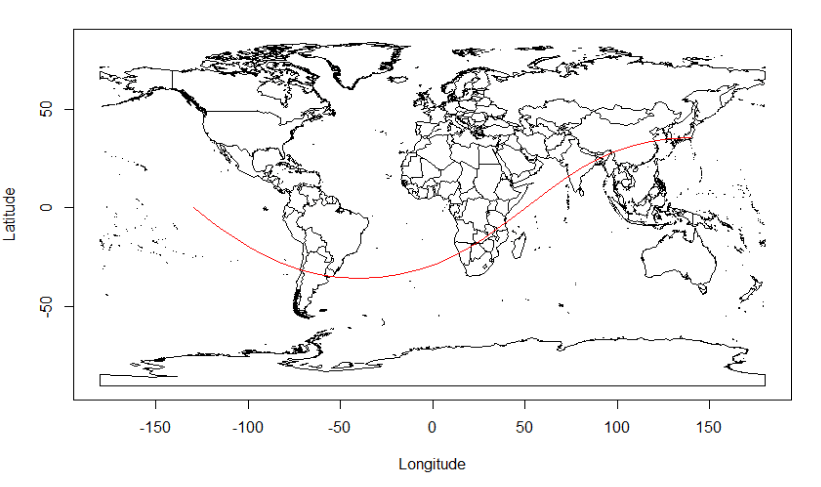
すると、以下の地図に示すように、東京で真西を向いた先には、インドやアフリカ南部などがあることが分かる。描かれ方が変な感じだと思われる方もいると思うが、球体である地球をむりやり平面の地図にしたためにこう描かれるのだ。気になった人は NHK for School の アメリカは日本の東?という動画を見てみよう。
応用2:同じ2000キロメートルのはずなのに?
ある地点からの等距離線、すなわち同じ距離だけ離れている場所をつなぎ合わせた線を描く方法について考えてみよう。ある地点からの等距離線上にある場所は、元々の地点との距離は同じであるが、方位だけが異なっている。よって、destPoint()函数を使うときに距離の値を変えずに、方位を少しずつ変えていけば等距離線を求めることができる。
例えば、経度0度線と赤道(緯度0度線)が交わる地点 p1 を考えよう。この地点からの2000キロメートル(200万メートル)の等距離線は、destPoint(p1, -180:180, 2000000) で求めることができる。ここで2つ目の引数の -180:180 が、方位を少しずつ変えていくことに相当する。真南(-180度)から、方位を1度ずつずらしていき、ぐるっと1周させるのである。なお、ここでは1度ずつずらしているが、もっと細かく描きたければ、0.5度ずつとか0.1度ずつずらしてもかまわない。
このことを踏まえて、経度0度線と赤道(緯度0度線)が交わる地点 p1 と、経度0度線と北緯45度線が交わる地点 p2 について、それぞれの地点から2000キロメートルの等距離線を描いて世界地図上に表してみよう。なお、p1 は西アフリカの沖合、p2 は西ヨーロッパに位置する。
# 地点の定義
p1 <- c(0,0)
p2 <- c(0,45)
# それぞれの地点から2000キロメートルの等距離線を求める
p1_circle <- destPoint(p1, -180:180, 2000000)
p2_circle <- destPoint(p2, -180:180, 2000000)
# 世界地図の描画
data(wrld)
plot(wrld, type = "l")
# それぞれの地点から2000キロメートルの範囲の描画
polygon(p1_circle, col = rgb(1, 0, 0, 0.3),
border = rgb(1, 0, 0, 1), lwd = 2)
polygon(p2_circle, col = rgb(0, 0, 1, 0.3),
border = rgb(0, 0, 1, 1), lwd = 2, lty = 2)
# それぞれの地点を示す点を書き加える
points(p1[1], p1[2], pch = 20, col = rgb(1, 0, 0, 1))
points(p2[1], p2[2], pch = 20, col = rgb(0, 0, 1, 1))
上記のスクリプトを処理すると、以下のような地図が描かれる。西アフリカの沖合を中心に赤い実線で囲まれたところが、p1 からの等距離線である。西ヨーロッパを中心に青い破線で囲まれたところが、p2 からの等距離線である。
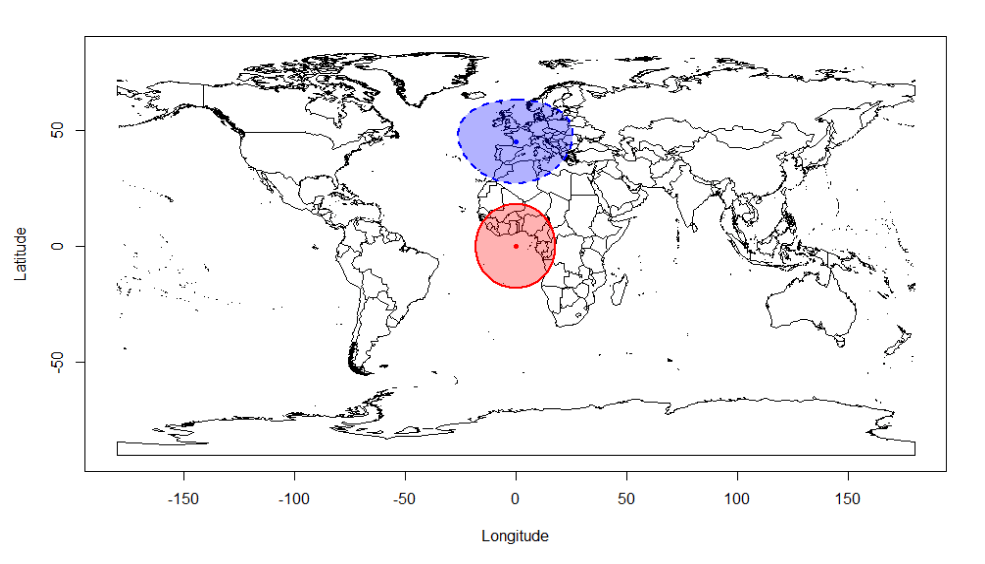
同じ2000キロメートルの等距離線であるものの、高緯度に位置する青く囲まれた部分の方がひずんで見える。これは、地球が丸いのにむりやり平らになるように地図を描いたため、高緯度の方がひずんでしまっているからである。
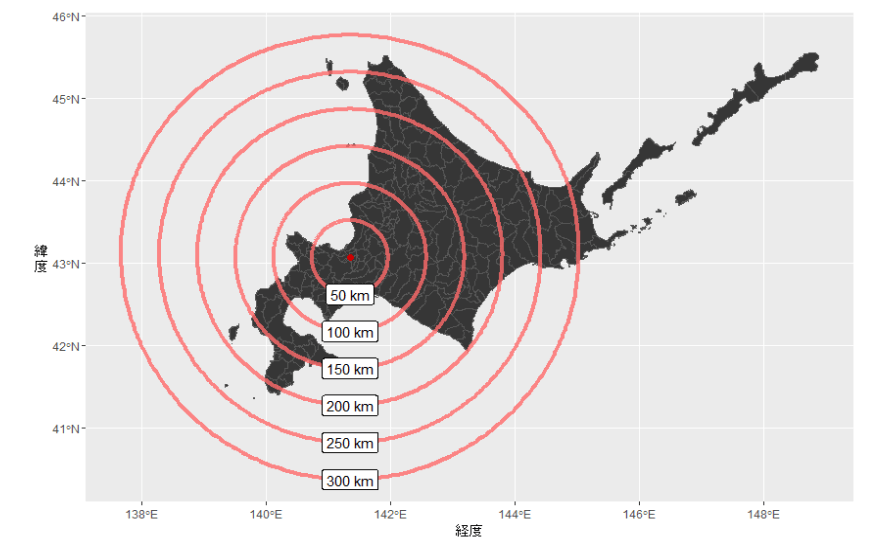
応用3:北海道はでっかいどう
もう1つ等距離線を描く例を挙げてみたい。北海道の地図上に、札幌駅から50, 100, …, 300キロメートルの等距離線を描きたいと思う。
日本の都道府県別の地図データを収めたパッケージとして、jpndistrict というものがある。このデータをもとに、ggplot2 パッケージの geom_sf() という函数を使って北海道の地図を描くことができる。なお、2018年5月25日現在、CRANに載っているggplot2 パッケージのバージョン2.2.1には geom_sf() が含まれていない。このため、GitHub に載っている開発中のバージョンを以下のようにしてあらかじめインストールしておく必要がある。
if(!require(devtools)){
install.packages("devtools")
}
devtools::install_github("tidyverse/ggplot2")
さて、実際に描いてみよう。等距離線を求めるに当たっては purrr パッケージの map_dfr() 関数を用いて、50キロメートルの等距離線から300キロメートルの等距離線のデータを1つのデータフレームにまとめるようにしている。また、等距離線を引くだけでは何キロメートルの等距離線か分からないので、札幌駅からの距離を示すラベルも描くようにしている。
library("jpndistrict")
library("tidyverse")
# 札幌駅の経度・緯度
sapporo <- c(141.350765, 43.068566)
# 札幌駅から50, 100, ..., 300キロメートルの等距離線を求める
sapporo_equidistant <-
map_dfr(1:6,
function(x){
destPoint(sapporo, -180:180, x*50000) %>%
as.tibble() %>%
# どの等距離線るかを示すグループ番号
mutate(group = as.character(x))
})
# 札幌駅からの距離を示すラベルの準備
sapporo_labels <-
map_df(1:6,
function(x){
destPoint(sapporo, 180, x*50000) %>%
as.tibble() %>%
mutate(distance = paste0(x*50, " km"))
})
# 図示
ggplot() +
# 北海道の地図の出力
geom_sf(data = jpn_pref(1), aes(geometry = geometry),
fill = "gray21", colour = "gray34") +
# 札幌駅から 50km, 100km, ..., 300km の等距離線の描画
geom_path(data = sapporo_equidistant,
aes(x=lon, y = lat, group = group),
colour = "indianred1", alpha=0.8, size = 1.5) +
# 札幌駅からの距離を示すラベルの描画
geom_label(data = sapporo_labels,
aes(x=lon, y = lat, label = distance)) +
# 札幌駅の位置を示す点の描画
annotate("point", x = sapporo[1], y = sapporo[2],
colour = "red3", size = 2) +
# 軸ラベル
xlab("経度") + ylab("緯\n度") +
theme(axis.title.y = element_text(angle = 0, vjust= 0.5))
結果は以下の通りである。