（西暦）2016（年）も（平成）28（年）も三角数かつ六角数

はじめに

まもなく、西暦で言うと2016年、和暦で言うと平成28年になる。この2016と28という数について、ちょっとした話をしたいと思う。

三角数

正三角形ができるように丸 ^[1] を並べてみよう。このとき、丸はいくつ必要になるだろうか。必要な丸の数は、正三角形の大きさによって変わってくる。小さな正三角形ならば必要な丸は少ないし、大きな正三角形ならば必要な丸は多くなる。とりあえず、小さなものから順に並べた例を見てみたいと思う ^[2] 。

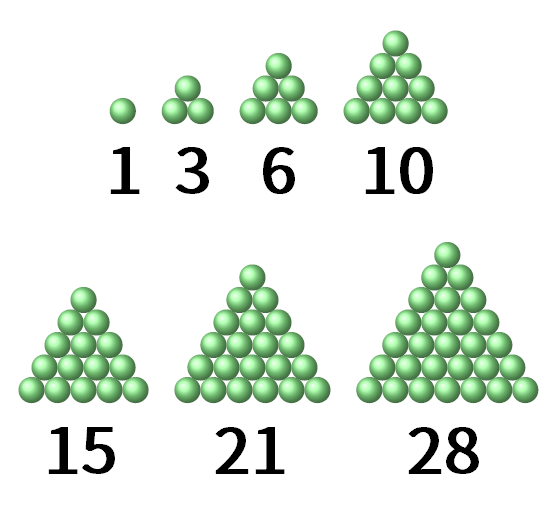
このように、正三角形に並べられる数のことを三角数という。上の図から明らかなように、三角数は小さいものから順に、1, 3, 6, 10, 15, 21, 28となる。つまり、1番目の三角数は1、2番目の三角数は3、3番目の三角数は6……ということになる。ここで先ほどの図を見直してみると、何番目の三角数かということは、並べてできあがった正三角形の1番外側の一辺の長さが丸何個分かということに対応している。一辺の長さが丸1個分ならば1番目の三角数 (1) に、丸2個分ならば2番目の三角数 (3) に、丸三個分ならば3番目の三角数 (6) に……といった形で対応している。

ここで、7番目の三角数が28になっていることに注目したい ^[3] 。来たる平成28年の28だ。

それでは、平成28年を西暦に換算した2016はどうなるだろうか。実は、2016も三角数だ。つまり、2016個の丸を正三角形ができるように並べることができる。実際に2016個の丸を正三角形の形に並べたものが以下の図だ。

ちなみに、三角数は、1から順に整数を足しあわせていった数に対応している ^[4] 。2番目の三角数は、1 + 2 = 3 となり、3番目の三角数は 1 + 2 + 3 = 6 となる。以下同様に、4番目の三角数なら 1 + 2 + 3 + 4 = 10 で、5番目の三角数なら 1 + 2 + 3 + 4 + 5 = 15 となる。

28は7番目の三角数だから、1 + 2 + 3 + 4 + 5 + 6 + 7 = 28 となる。そして、2016は63番目の三角数だから、1 + 2 + 3 + … + 62 + 63 = 2016 となるわけだ。

六角数

正三角形の代わりに他の正多角形をなすように丸を並べることも考えることができる。ある正多角形を並べるときに必要な丸の数のことをその多角数と呼ぶ。例えば、正六角形ができるように丸を並べたときに、必要となる丸の数は六角数と呼ばれる。

このような言葉だけの説明だと想像しにくい人もいるだろう。まずは具体的に並べた例を見るのが分かりやすいと思う。以下は、正六角形になるように丸を並べた例だ。

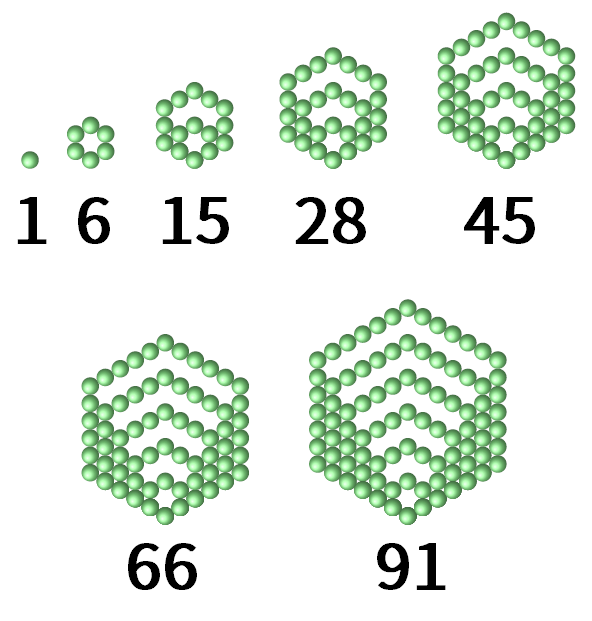
ここで28は4番目の六角数になっている。それでは、2016はどうか。実は2016は32番目の六角数だ。実際に2016個の丸を正六角形の形に並べたものが、以下の図だ。

なお、全ての六角数は三角数である ^[5] 。つまり、ある数が六角数だと分かった時点で、その数は三角数でもあるということが分かる。なので、28も2016も六角数である以上、三角数でもあることは不思議なことでも何でもない。

2016はさまざまな多角数になっている

2016は、63番目の三角数、32番目の六角数であるほかに、14番目の二十四角数、6番目の百三十六角数、3番目の六百七十三角数、2番目の二千十六角数でもある。つまり、2016は、6種類の多角数になっている。

西暦の年数が6種類以上 ^[6] の多角数になっている数であるのは久しぶりだ。2016の前は1701 ^[7] なのだ。そして、2016の次は2556 ^[8] になる。

ちなみに、28は3種類の多角数だ。すなわち、7番目の三角数、4番目の六角数、2番目の二十八角数である。

もう少し数学的な説明

一般に $i$ 番目の $n$ 角数は $\displaystyle\frac{(n-2)i^{2} – (n-4)i}{2}$ で求められる（ただし $i$ は正の整数で $n$ は3以上の整数とする）。例えば $i = 7, n=3$ としてこの公式に当てはめれば、7番目の三角数は $\displaystyle\frac{(3-2)7^{2} – (3-4)7}{2} = 28$ となることが分かる。

この公式を使えば、正の整数 $m$ が何種類の多角数になっているかという問題は、 $m = \displaystyle\frac{(n-2)i^{2} – (n-4)i}{2}$ を満たす $(i, n)$ の組み合わせがいくつあるかという問題と同じことになる。

付：素数な日付

西暦

西暦の年月日をまとめて1つの数字にしたときに素数となる日付は、2016年（平成28年）には19個存在する。

1. 2016年03月19日 → 20160319 → 素数
2. 2016年04月01日 → 20160401 → 素数
3. 2016年04月03日 → 20160403 → 素数
4. 2016年05月29日 → 20160529 → 素数
5. 2016年06月01日 → 20160601 → 素数
6. 2016年06月07日 → 20160607 → 素数
7. 2016年06月11日 → 20160611 → 素数
8. 2016年07月09日 → 20160709 → 素数
9. 2016年07月27日 → 20160727 → 素数
10. 2016年08月09日 → 20160809 → 素数
11. 2016年08月17日 → 20160817 → 素数
12. 2016年08月21日 → 20160821 → 素数
13. 2016年09月23日 → 20160923 → 素数
14. 2016年10月07日 → 20161007 → 素数
15. 2016年10月13日 → 20161013 → 素数
16. 2016年10月19日 → 20161019 → 素数
17. 2016年10月21日 → 20161021 → 素数
18. 2016年10月27日 → 20161027 → 素数
19. 2016年11月03日 → 20161103 → 素数

和暦

和暦の年月日をまとめて1つの数字にしたときに素数となる日付は、2016年（平成28年）には32個存在する。

1. 28年01月03日 → 280103 → 素数
2. 28年01月21日 → 280121 → 素数
3. 28年01月29日 → 280129 → 素数
4. 28年02月07日 → 280207 → 素数
5. 28年02月19日 → 280219 → 素数
6. 28年02月23日 → 280223 → 素数
7. 28年02月29日 → 280229 → 素数
8. 28年03月03日 → 280303 → 素数
9. 28年03月21日 → 280321 → 素数
10. 28年03月27日 → 280327 → 素数
11. 28年04月09日 → 280409 → 素数
12. 28年04月11日 → 280411 → 素数
13. 28年05月07日 → 280507 → 素数
14. 28年05月13日 → 280513 → 素数
15. 28年06月03日 → 280603 → 素数
16. 28年06月07日 → 280607 → 素数
17. 28年06月13日 → 280613 → 素数
18. 28年06月27日 → 280627 → 素数
19. 28年07月03日 → 280703 → 素数
20. 28年07月11日 → 280711 → 素数
21. 28年07月17日 → 280717 → 素数
22. 28年07月29日 → 280729 → 素数
23. 28年08月11日 → 280811 → 素数
24. 28年08月17日 → 280817 → 素数
25. 28年09月09日 → 280909 → 素数
26. 28年09月13日 → 280913 → 素数
27. 28年09月21日 → 280921 → 素数
28. 28年09月27日 → 280927 → 素数
29. 28年10月23日 → 281023 → 素数
30. 28年11月17日 → 281117 → 素数
31. 28年12月07日 → 281207 → 素数
32. 28年12月27日 → 281227 → 素数

なお、西暦でも和暦でも素数になるのは、06月07日 (20160607, 280607)、08月17日 (20160817, 280817)の2日のみである。

付：28は完全数

ちなみに、28は完全数だ。完全数とは、ある整数の約数をその整数自身を除いて足しあわせたものが、その整数に等しくなる数のことである。28の約数は、1, 2, 4, 7, 14, 28 である。28を除いた5つの約数を足しあわせると、1 + 2 + 4 + 7 + 14 = 28 ともとの整数と等しくなる ^[9] 。完全数は結構めずらしい数だ。小さいものから順に挙げると、6, 28, 496, 8128, 33550336, 8589869056, 137438691328, 2305843008139952128……となる。

28が完全数だという話は、第1回本屋大賞を受賞した小川洋子の小説『博士の愛した数式』の主題の1つにもなっている。平成28年という年の表す数字に興味が持てた人は読んでみてもよいかもしれない。

1. 並べるものは別に丸に限る必要なないのだが、この記事では便宜上丸を並べている。 [↩]
2. 以下の図を描くにあたっては、Stack Exchange の Triangular numbers in TikZ という質問とそれに対する回答を参考にした [↩]
3. これは、先ほどの図で1番外側の一辺の長さが丸7個分の正三角形は、合計28個の丸で作られていることに対応している。 [↩]
4. 数式を用いて表せば、 $i$ 番目の三角数は $1 + 2 + \cdots + i$ となる。つまり、$i$ 番目の三角数は $\displaystyle\sum_{k=1}^i k = \frac{1}{2}i(i+1)$ となる。 [↩]
5. 逆に三角数は六角数であるとは限らない。 [↩]
6. 1を除く3000以下の整数では、高々7種類の多角数にしかならない。1を除く3000以下の整数の中で、7種類の多角数になっているのは1225と1540のみである。また、6種類の多角数になるのは、561, 1485, 1701, 2016, 2556, 2601, 2850の7つの数のみである。ちなみに、1は任意の多角数の1番目である。つまり、三角数の1番目であり、四角数の1番目であり、五角数の1番目であり……ということになる。 [↩]
7. 1701は、6種類の多角数になっている。すなわち、1701は、21番目の十角数、18番目の十三角数、9番目の四十九角数、6番目の百十五角数、3番目の五百六十八角数、2番目の千七百一角数である。 [↩]
8. 2556は、6種類の多角数になっている。すなわち、2556は、71番目の三角数、36番目の六角数、8番目の九十三角数、6番目の百七十二角数、3番目の八百五十三角数、2番目の二千五百五十六角数である。 [↩]
9. 2016は完全数ではない。2016の約数は、1, 2, 3, 4, 6, 7, 8, 9, 12, 14, 16, 18, 21, 24, 28, 32, 36, 42, 48, 56, 63, 72, 84, 96, 112, 126, 144, 168, 224, 252, 288, 336, 504, 672, 1008, 2016 であり、2016以外を足しあわせると 4536 となる。ある整数の約数をその整数自身を除いて足しあわせたものが、その整数より大きくなる数は過剰数と呼ばれる。つまり、2016は過剰数の1つである。 [↩]