はじめに
明治三十九年度(1906年度)の旧制高等学校の入試問題のなかから数学の問題を紹介する。当時、日本には第一高等学校から第七高等学校までの7つの高等学校があり、入試問題は共通であった。
なお、旧制の高等学校は、「高等学校」という名前はついているものの、現在の高等学校とは位置づけが異なる学校である。あえて現在の学校制度の中で位置づけるとすれば、大学の教養課程に相当すると考えてよい。
当時の入試は、7月に行われた。9月に入学することになっていたため、入試は夏に行われたのだ。数学に関する部分で言うと、算術・代数・幾何・三角法の四分野がバランスよく出されている。この四分野がバランスよく出題されているのは、明治期の高等学校の入試の特徴である。大正の後半からは、算術と三角法がほとんど出されなくなる。
算術
問1
問1は単純な文章題である。現在ならば中学入試に出題されてもおかしくないレベルだ。
一 甲乙丙三人池ノ周圍ヲ散步スルニ甲ハ八分乙ハ十二分丙ハ十六分ニテ一周スト云フ今三人同時ニ此池ノ周圍ノ一點ヲ出發シ上記ノ速サニテ池ヲ廻ルトシ再ヒ出發點ニ於イテ三人一處ニナルマデノ時閒ヲ問フ
(現代語訳:池の周りを一周するのに、甲は8分、乙は12分、丙は16分かかる。3人が池の周囲の同じ場所から同時に上記の早さで歩くとしたら、出発点で再び3人が一緒になるのはいつか。)
この問題は非常に簡単で、8と12と16の公倍数を求めれば良いだけである。これら3つの数の公倍数は48なので、答えは48分となる。
問2
問2は比に関する文章題である。
二 甲ナル人二千圓ノ資金ヲ以テ或ル商業ヲ開始シタリ乙ハ三箇月經過ノ後三千丙ハ其ノ後更ニ三箇月經過ノ後四千五百圓ノ資金ヲ出シテ甲ト共同シテ同業ニ從事シタルニ創業ヨリ一箇年ノ後二千五百圓ノ純益ヲ得タリ此內二割五分ヲ積立金トシ殘額ヲ出金額及ビ投資ノ期閒ニ應ジテ三人ニテ分配セントス各人ノ所得ヲ求ム
(現代語訳:甲という人が2000円の資金である商売を始めた。乙はその3ヶ月後に3000円、丙はさらにその3ヶ月後に4500円の資金を出して、甲と一緒に商売に従事した。商売を始めてから1年後に2500円の純益を得た。このうち2割5分を積立金として残額を出資額と投資期間に応じて3人で分配しようとしている。3人得る金額はがそれぞれいくらか。)
現代の感覚からすると2000円しか出資しないというのは少なすぎると感じる人もいるかもしれないが、この問題が出された時は物価が安かったので2000円の出資というのは決して少なくない。例えば、この試験が行われた翌年の1907年(明治40年)に夏目漱石が朝日新聞社に入社した際の月給は200円であるから、2000円というのはかなりの大金である。
2500円の純益のうち、2割5分(25%)を積立金として残すので、積立金の金額は、2500×0.25=625(円)となる。よって、分配対象となる残金は2500–625=1875(円)である。 この1875円を3人の出資額と投資期間に応じて分配すれば良いのだ。ここでは出資額と投資期間をかけ算することでそれぞれの分配比率が分かる。甲については 2000円×12ヶ月=24000、乙については 3000円×9ヶ月=27000、丙については 4500円×6ヶ月=27000 となり、つまり甲・乙・丙3人の分配比率は24000:27000:27000となる。この比を簡単にすると、甲・乙・丙で8:9:9となる。よって、分配対象の全体を26とすると、そのうちの8が甲のもの、9が乙のもの、9が丙のものとなる。
つまり、分配対象となる残金1875円のうち、甲はその26分の8、乙はその26分の9、丙はその26分の9を得ることになる。
- 甲が得る金額:1875×8/26 ≒ 576.92円。すなわち、576円92銭。
- 乙が得る金額:1875×9/26 ≒ 649.04円。すなわち、649円4銭。
- 丙が得る金額:1875×9/26 ≒ 649.04円。すなわち、649円4銭。
なお、1875円は26で割り切れないので、答えを求める際には四捨五入する必要がある。
代数
問1
代数の問1は、平方根を含む分数式を計算する問題である。
一
\[\frac{2\sqrt{15}+8}{5+\sqrt{15}} \div \frac{8\sqrt{3}-6\sqrt{5}}{5\sqrt{3}-3\sqrt{5}}\]ヲ最簡形ニ化セヨ
面倒な式だが、着実に計算して行けばそれほど難しい問題ではない。
\begin{eqnarray} && \frac{2\sqrt{15}+8}{5+\sqrt{15}} \div \frac{8\sqrt{3}-6\sqrt{5}}{5\sqrt{3}-3\sqrt{5}} \\ &=& \frac{\left(2\sqrt{15}+8\right)\left(5\sqrt{3}-3\sqrt{5}\right)}{\left(5+\sqrt{15}\right)\left(8\sqrt{3}-6\sqrt{5}\right)} \\ &=& \frac{30\sqrt{5}-30\sqrt{3}+40\sqrt{3}-24\sqrt{5}}{40\sqrt{3}-30\sqrt{5}+24\sqrt{5}-30\sqrt{3}} \\ &=& \frac{10\sqrt{3}+6\sqrt{5}}{10\sqrt{3}-6\sqrt{5}} \end{eqnarray}ここまで求めたら、あとは分母を有理化するだけだ。
\begin{eqnarray} &=& \frac{\left(10\sqrt{3}+6\sqrt{5}\right)^{2}}{\left(10\sqrt{3}-6\sqrt{5}\right)\left(10\sqrt{3}+6\sqrt{5}\right)} \\ &=& \frac{300+120\sqrt{15}+180}{300-180} \\ &=& \frac{480+120\sqrt{15}}{120} \\ &=& 4 + \sqrt{15} \end{eqnarray}問2
代数の問1は、連立方程式を解くだけの問題である。
二 次ノ聯立方程式ヲ解ケ
\begin{eqnarray} x^{2}y + y^{2}x &=& 30 \\ \frac{1}{x} + \frac{1}{y} &=& \frac{5}{6} \end{eqnarray}
この連立方程式も面倒なだけで、根気よく計算して行けば解くのは難しくない。
まず第1の方程式を変形すると、以下のようになる。
\begin{eqnarray} x^{2}y + y^{2}x &=& 30 \\ xy(x+y) &=& 30 \end{eqnarray}第2の方程式については両辺に$xy$を掛けることで、以下のようになる。
\begin{eqnarray} \frac{1}{x} + \frac{1}{y} &=& \frac{5}{6} \\ x +y &=& \frac{5}{6}xy \end{eqnarray}ここで $x+y = \alpha, xy = \beta$ と置けば、元々の連立方程式を以下のような$\alpha, \beta$に関する連立方程式に置き換えることができる。
\begin{eqnarray} \alpha\beta &=& 30 \\ \alpha &=& \frac{5}{6}\beta \end{eqnarray}ここで $\alpha = \frac{5}{6}\beta$ を $\alpha\beta = 30$ に代入すると、$\frac{5}{6}\beta^{2} = 30$ となる。よって、$\beta = \pm 6$となる。すなわち、$\alpha = 5, \beta =6$ もしくは $\alpha = -5, \beta =-6$ が解として得られる。
$\alpha = 5, \beta =6$ であるとき、以下の連立方程式が得られる。
\begin{eqnarray} x+y &=& 5 \\ xy &=& 6 \end{eqnarray}これを解くと、$x = 2, y = 3$ もしくは $x = 3, y = 2$ が解となることが分かる。
また、$\alpha = -5, \beta = -6$ であるとき、以下の連立方程式が得られる。
\begin{eqnarray} x+y &=& -5 \\ xy &=& -6 \end{eqnarray}これを解くと、$x = 1, y = -6$ もしくは $x = -6, y = 1$ が解となることが分かる。
よって、以下の4通りの解が得られる。
- $x = 2, y = 3$
- $x = 3, y = 2$
- $x = 1, y = -6$
- $x = -6, y = 1$
幾何
問1
幾何の問1は平面図形に関する証明問題である。
一 $ABC$ヲ圓ニ內接スル正三角形トシ$P$ヲ弧$BC$ノ上ニアル任意ノ點トスルトキハ$PA=PB+PC$ナルコトヲ證明セヨ
(現代語訳:$ABC$を円に内接する正三角形とし、$P$を弧$BC$上にある任意の一点とする。このとき、$PA=PB+PC$となることを証明しなさい。)
問題の状況を図に表すと以下のようになる。
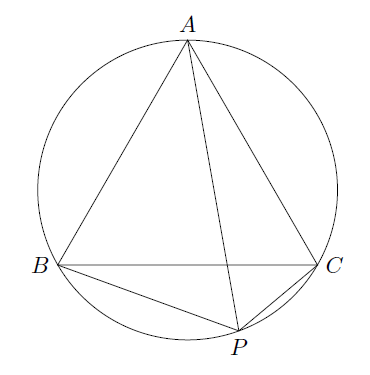
ここで、$PA$ 上に、$PC = PQ$ となるような点 $Q$ を置く。このとき、三角形$AQC$と三角形$BPC$が合同であることから、$AQ = BP$ となる。よって、$AQ + PQ = PA = PB + PC$ となる。
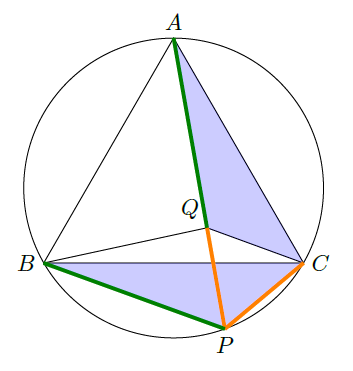
三角形$AQC$と三角形$BPC$が合同であることは以下のように証明する。
まず、$\angle APC$ は弧$AC$に対する円周角である。弧$AC$ は円周全体の3分の1を占めるからその円周角は、60°になる。三角形$PQC$ は $PQ=PC$の二等辺三角形であり、しかも頂角が60°となることから、正三角形である。よって、$QC = PC$となる。
さらに、$\angle ACQ = 60^{\circ} – \angle BCQ = \angle BCP$ であり、三角形$ABC$が正三角形であることから$AC = BC$となる。すなわち、二辺とその間の角が等しいから、三角形$AQC$と三角形$BPC$は合同である。
問2
幾何の問2は簡単な作図問題である。
二 相交ハラザル二直線ニ出會ヒ且双方ニ垂直ナル直線ヲ引ケ
(現代語訳:交わらない二直線がある。この二直線の双方に対して垂直になる直線を引きなさい。)
ここでの「相交ハラザル二直線」(交わらない二直線)は平面上の話なのか、空間上の話なのか指定されておらず、どう問題を解釈するか悩むところである。だが、とりあえず、(ユークリッド幾何学における)平面上の話をしているものと考えよう。平面上ならば、交わらない二直線というのは要するに平行な二直線のことである [1] 。
こう考えると、この問題は平行な二直線に対して垂直な線を作図する問題ということになる。
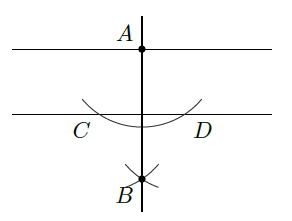
それでは、作図方法を示そう。まず、平行な二直線の片方の任意の場所に点$A$を置く。次に、点$A$を中心として、もう片方の直線と2カ所で交わるように円弧を描く。こうして交わった二点を$C, D$とする。
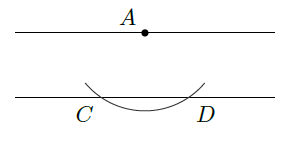
さらに、$C, D$それぞれを中心とする同一半径の円弧を描き、その交点を$B$とする。最後に直線$AB$を結べば、これが交わらない二直線に対して垂直となる直線である。
三角法
問1
三角法の問1は三角比を用いて、長さを求める問題である。
直立セル一塔アリ其ノ底ヲ通ズル水平面上ノ一點ニテ其ノ頂ヲ見レバ仰角32°27′ナリ此ノ點ヨリ塔ニ向ツテ同平面上尙100尺ヲ進ミタル點ニテ頂ヲ見レバ仰角45°ナリ此平面上塔ノ高サ幾尺ナルカ但シ tan 32°20′= 0.6330, tan 32°30′= 0.6371ナリトス
(現代語訳:直立する塔が1つある。その底面と同じ水平面上の一点からその塔の一番高いところを見たところ、仰角は32°27′であった。この点から塔に向かって同一平面上を100尺進んだ点から一番高いところを見たところ、仰角は45°であった。この平面上の塔の高さは何尺か。ただし、 tan 32°20′= 0.6330, tan 32°30′= 0.6371 とする。)
尺は昔の日本で使われていた長さの単位で、一尺は33分の10メートルに相当する。
まず、塔への仰角が32°27′であった地点を$A$とし、45°であった地点を$B$とする。さらに塔の底を$C$とし、塔の一番高いところを$D$とすれば、この問題の状況を以下の図のように表すことができる。
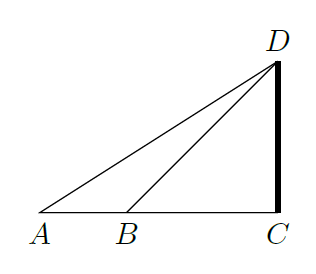
さて、塔の高さを$x$尺と置こう。すなわち、$CD = x$ とする。ここで、$BCD$は二等辺直角三角形だから、$CD = BC = x$となる。$AB = 100$ だから、$AC = x + 100$ である。また、タンジェントの定義から $\tan A = \frac{CD}{AC}$ となる。
よって、$\tan A = \frac{x}{x +100}$ となる。これを$x$について解くと、$x = \frac{-100 \tan A}{\tan A -1}$ となる。あとは、$\tan A$ の値、すなわち、tan 32°27′ を求めれば良い。tan 32°27′ の値は与えられていないが、tan 32°20′= 0.6330, tan 32°30′= 0.6371から線形補間で求めれば、tan 32°27′ はおよそ 0.6358 となることが分かる。よって、$x = \frac{-100 \tan A}{\tan A -1}$ に代入すれば、この塔の高さが 174.6 尺であると分かる。
この問題が出された頃は、タンジェントを求める時には数表を使っていたので、数表に載っていない値を線形補間で求める必要があったのだ。
問2
三角法の問2は証明問題である。
$\cos A = \frac{\cos B – k}{1-k\cos B}$ ナルトキハ $\tan\frac{A}{2} = \sqrt{\frac{1+k}{1-k}}\tan\frac{B}{2}$ ナルコトヲ證明セヨ
(現代語訳:$\cos A = \frac{\cos B – k}{1-k\cos B}$ が成立するとき $\tan\frac{A}{2} = \sqrt{\frac{1+k}{1-k}}\tan\frac{B}{2}$ となることを証明しなさい。)
この証明問題は実は証明ができない。反例があるのだ。例えば、$A = 240^{\circ}, B= 90^{\circ}, k = \frac{1}{2}$ とすれば、$\cos A = \frac{\cos B – k}{1-k\cos B}$ は成り立つ。しかし、このとき$\tan\frac{A}{2} = \sqrt{\frac{1+k}{1-k}}\tan\frac{B}{2}$ は成立しない。左辺は$-\sqrt{3}$となるのに対し、右辺は $\sqrt{3}$ となるのだ [2] 。
もししっかりとした証明問題にしたかったら、出題の際に$A, B$の取りうる値を限定しなくてはならない。